I just attended a great talk by Laura McLay at the German OR Society meeting in Aachen. In her semi-plenary, Laura talked about all the work she has done in Emergency Medical Response. Planning the location and operation of ambulances, fire trucks, emergency medical technicians, and so on is a difficult problem, and Laura has made very good progress in putting operations research to use in making systems work better. She has been recognized for this work not only in our field (through things like outstanding paper awards and an NSF CAREER award) but also by those directly involved in emergency response planning, as evidenced by an award from the National Association of Counties.
Laura covered a lot of ground in her talk (she has a dozen papers or more in the area), but I found one result in particular very striking. Many ambulance systems have a goal of responding to 80% of their calls in 9 minutes (or some such numbers). One of the key drivers of those values is the survivability from heart attacks: even minutes matter in such cases.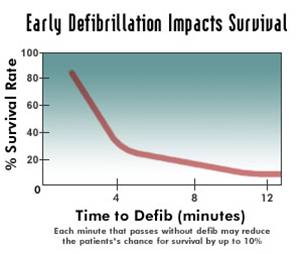 The graph attached (not from Laura, available in lots of places on the internet) shows a sharp dropoff as the minutes tick away.
The graph attached (not from Laura, available in lots of places on the internet) shows a sharp dropoff as the minutes tick away.
But why 9 minutes? It is clear from the data that if the goal is to provide response within 9 minutes, there is an awful lot of 8 minute 30 second response times. Systems respond to what is measured. Wouldn’t it be better, then to require 5 minute response times? Clearly more people would be saved since more people would be reached within the critical first minutes. This looks like a clear win for evidence-based medicine and the use of analytics in decision making.
But Laura and her coauthors have a deeper insight than that. In the area they are looking at, which is a mix of suburban and rural areas, with a 9 minute response time, the optimal placement of ambulances is a mixture of suburban and rural locations. With a 5 minute response time, it does no good to place an ambulance in a rural location: they can’t get to enough people in time. All the ambulances would be placed in the higher-density suburban location. If a call comes in from a rural location, eventually an ambulance would wend its way to the rural location, but after 20 or 30 minutes, many cases become moot.
To figure out the optimal response time, you need to figure out both survivability and the number of cases the system can reach. For the area Laura and her team looked at, the optimal response time turned out to be 8 to 9 minutes.
Of course, this analysis is not relevant if the number of ambulances is increased with the decreased response time requirement. But the enthusiasm for spending more on emergency response is not terrifically high, so it is more likely that the time will be changed without a corresponding increase in budget. And that can have the effect of making the entire system worse (though things are better for the few the ambulance can reach in time).
This was a great example of the conflict between individual outcome and social outcomes in emergency response. And a good example of how careful you need to be when using analytics in health care.
I highly recommend reading her Interfaces article “Hanover County Improves its Response to Emergency Medical 911 Patients” (no free version). I even more highly recommend her blog Punk Rock Operations Research and her twitter stream at @lauramclay.