Suggested Research Projects

1. Implement and test algorithms from the literature. Our references contain many papers that already do this, and these should be examined closely before undertaking a study of this sort, but there is still room for such studies. One can implement theoretical algorithms not previously studied experimentally, compare algorithms that performed well in earlier studies but had not previously been directly compared, test old algorithms on new test beds, etc.

2. Use detailed profiling of an algorithm's implementation to better understand the circumstances that make it perform well or poorly, and to help extrapolate performance to very large instances sizes.

3. Design new algorithms for the problems and compare them to the previous best. These could involve substantially new algorithmic ideas or simply more efficient use of tuned data structures.

4. Adapt general purpose heuristic methods (such simulated annealing[81][56][31][23][1], tabu search [49][43], and genetic algorithms [44]), to the clique and/or coloring problems. Some work has already been done along these lines, as cited above, but typically there are a variety of ways in which one of these approaches can be adapted to a particular problem, and such new adaptations can be compared to previous techniques.

5. Examine neighborhood structures for local search. One aspect of these problems that makes solution difficult is the lack of a natural neighborhood structure for local search. Neighborhood structures for these problems tend either to be too narrow (leading to poor local optima) or too broad (leaving a difficult neighborhood problem). What are some alternative neighborhoods and how can they be effectively searched?

6. Explore the role of randomization. Most of the algorithms created are completely deterministic. Can randomization help in solving these types of problems?

7. Experiment on alternative machine architectures, including parallel and vector processors. How can multiple processors be exploited in solving these problems? This could be either via distributed computing (generally with high communications costs, heterogeneous machines, and/or limited connectivity) or with such special purpose machines as Connection Machine computers.

8. Examine real world problems. The clique problem is commonly claimed to have widespread applicability. Most computational work to date, however, has been done with random graphs. How do real world problems differ from such random graphs? How would the conclusions drawn from past research be different if real problems were solved? Identify a real-world application from which you can obtain instance data, and then answer the above questions.

9. Create and examine alternative instance generators. Consider the ``geometric graphs'' of [53], where the nodes of a graph as points in the Euclidean plane where an edge occurs only if the corresponding nodes are sufficiently close (or sufficiently far away). Consider also the generators proposed in [48]. Are these interesting problem generators? Do algorithms perform well or poorly for them? What other generators have interesting properties? (One ``product'' we hope this Challenge to produce is a broad library of generators and real-world instances for future researchers to use.)

10. Examine ``pathological'' examples. For each optimization algorithm developed, there is a class of examples for which the algorithm does well and a class for which it does poorly. Can you characterize why an algorithm does poorly? Alternatively, can you determine a large, interesting, class for which certain algorithms work well?

11. Examine planar graphs. The four color theorem, as proved by [4][3] is actually a constructive theorem that gives an 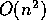algorithm for 4-coloring a graph. This algorithm seems completely impractical due to the large constants involved. Morgenstern and Shapiro [70] provide some heuristics for such graphs and might be seen as a starting point for this class of interesting graphs.

12. Examine more fundamental issues in computational testing using these problems as a testbed. How should algorithms and heuristics be compared across environments? Does good computational work require outstanding ``hacking'' ability, or is there some more fundamental measure independent of implementation?.