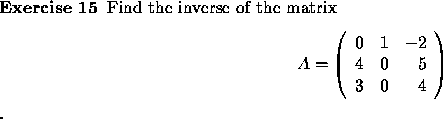
If A and B are square matrices such that
AB = I (the identity matrix),
then B is called the inverse of A and is denoted
by ![]() .
A square matrix A has either no inverse or a unique
inverse
.
A square matrix A has either no inverse or a unique
inverse ![]() . In the first case, it is said to be
singular and in the second case nonsingular.
Interestingly, linear independence of vectors plays a
role here: a matrix is singular if its columns form a
set of linearly dependent vectors; and it is nonsingular
if its columns are linearly independent.
Another property is the following:
if B is the inverse of A, then A is the inverse of B.
. In the first case, it is said to be
singular and in the second case nonsingular.
Interestingly, linear independence of vectors plays a
role here: a matrix is singular if its columns form a
set of linearly dependent vectors; and it is nonsingular
if its columns are linearly independent.
Another property is the following:
if B is the inverse of A, then A is the inverse of B.
An important property of nonsingular square matrices is the following. Consider the system of linear equations
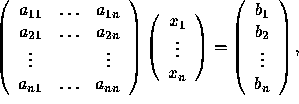 simply written as Ax = b.
simply written as Ax = b.
When A is a square nonsingular matrix,
this linear system has a unique solution, which can be obtained as follows.
Multiply the matrix equation Ax = b by ![]() on
the left:
on
the left:
![]()
This yields ![]() and so, the unique solution to the
system of linear equations is
and so, the unique solution to the
system of linear equations is
![]()

Finding the Inverse of a Square Matrix
Given 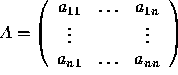 ,
we must find
,
we must find 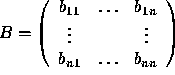 such that AB = I (the identity matrix).
Therefore, the first column of B must satisfy
such that AB = I (the identity matrix).
Therefore, the first column of B must satisfy 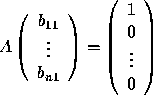 (this vector is the 1st column of I). Similarly, for the other
columns of B. For example, the jth column of B satisfies
(this vector is the 1st column of I). Similarly, for the other
columns of B. For example, the jth column of B satisfies
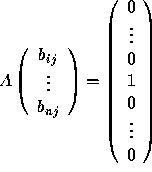 (the jth column of I). So
in order to
get the inverse of an
(the jth column of I). So
in order to
get the inverse of an ![]() matrix, we must solve n linear
systems. However, the same steps of the Gauss-Jordan elimination
procedure are
needed for all of these systems. So we solve them all at once,
using the matrix form.
matrix, we must solve n linear
systems. However, the same steps of the Gauss-Jordan elimination
procedure are
needed for all of these systems. So we solve them all at once,
using the matrix form.
Example: Find the inverse of 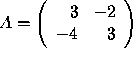 .
.
We need to solve the following matrix equation
![]()
We divide the first row by 3 to introduce a 1 in the top left corner.
![]()
Then we add four times the first row to the second row to introduce a 0 in the first column.
![]()
Multiply the second row by 3.
![]()
Add ![]() the second row to the first. (All this is
classical Gauss-Jordan elimination.)
the second row to the first. (All this is
classical Gauss-Jordan elimination.)
![]()
As IB = B, we get
![]()
It is important to note that, in addition to the two elementary row operations introduced earlier in the context of the Gauss-Jordan elimination procedure, a third elementary row operation may sometimes be needed here, namely permuting two rows.
Example: Find the inverse of 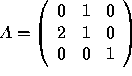 .
.
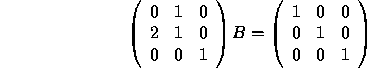
Because the top left entry of A is 0, we need to permute rows 1 and 2 first.
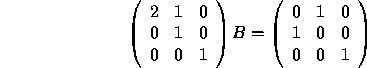
Now we divide the first row by 2.
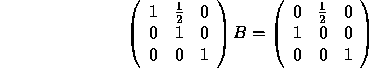
Next we add ![]() the second row to the first.
the second row to the first.
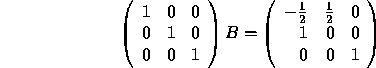
and we are done, since the matrix in front of B is the identity.