Global Optima

Finding global maxima and minima is harder. There is one case that is of interest.

We say that a domain is convex if every line drawn between two points in the domain lies within the domain.

We say that a function f is convex if the line connecting any two points lies above the function. That is, for all x,y in the domain and , we have , as before (see Chapter 2).

• If a function is convex on a convex domain, then any local minimum is a global minimum.
• If a function is concave on a convex domain, then any local maximum is a global maximum.

To check that a function is convex on a domain, check that its Hessian matrix H(x) is positive semidefinite for every point x in the domain. To check that a function is concave, check that its Hessian is negative semidefinite for every point in the domain.

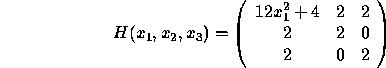
The determinants of the principal minors are det , det and det . So is positive semidefinite for all in . This implies that f is convex over .