Next: Solution of Linear Programs
Up: The Simplex Method
Previous: The Simplex Method
Before we start discussing the simplex method, we point out that
every linear program can be converted into ``standard'' form
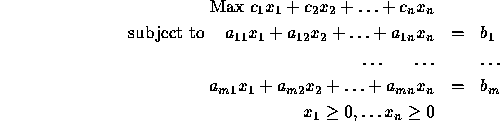
where the objective is maximized, the constraints are equalities
and the variables are all nonnegative.
This is done as follows:
- If the problem is min z, convert it to max -z.
-
If a constraint is
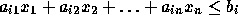 ,
convert it into an equality constraint by adding a nonnegative slack
variable
,
convert it into an equality constraint by adding a nonnegative slack
variable 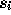 . The resulting constraint is
. The resulting constraint is
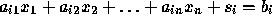 , where
, where 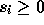 .
. -
If a constraint is
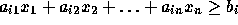 ,
convert it into an equality constraint by subtracting a nonnegative
surplus variable
,
convert it into an equality constraint by subtracting a nonnegative
surplus variable 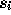 . The resulting constraint is
. The resulting constraint is
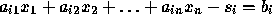 , where
, where 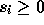 .
. -
If some variable
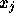 is unrestricted in sign, replace it everywhere in
the formulation by
is unrestricted in sign, replace it everywhere in
the formulation by 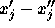 , where
, where 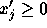 and
and 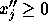 .
.
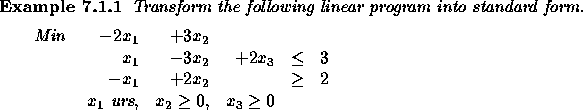
Let us first turn the objective into a max and the constraints into
equalities.
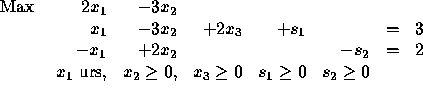
The last step is to convert the unrestricted variable 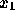 into
two nonnegative variables:
into
two nonnegative variables: 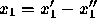 .
.
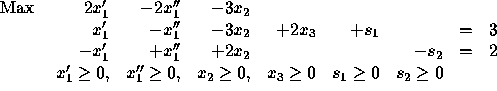
Michael A. Trick
Mon Aug 24 16:30:59 EDT 1998
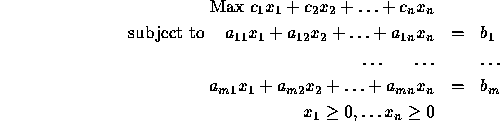
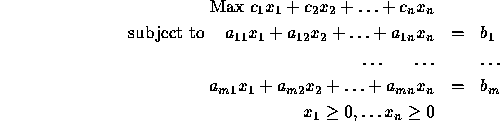
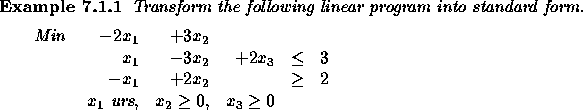
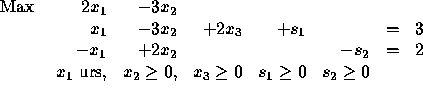
![]() into
two nonnegative variables:
into
two nonnegative variables: ![]() .
.