Exercises

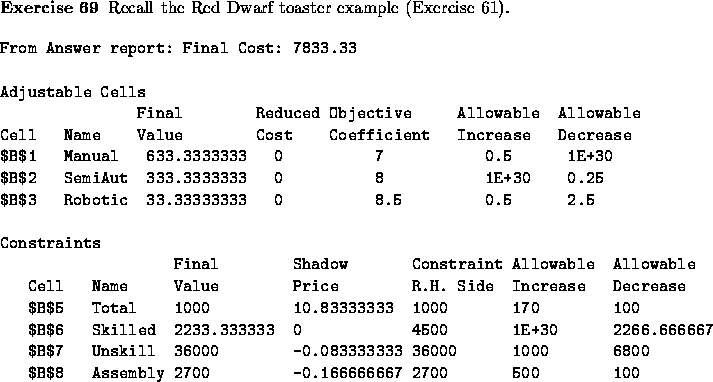
(a) What is the optimal allocation of production? What is the average cost/toaster of production.

(b) By how much can the cost of robots increase before we will change that production plan.

(c) How much is Red Dwarf willing to pay for more assembly room time? How many units is Red Dwarf willing to purchase at that price?

(d) How much will we save if we decide to produce only 950 toasters?

(e) A new production process is available that uses only 2 minutes of skilled labor, 10 minutes of unskilled labor, and an undetermined amount of assembly floor time. Its production cost is determined to be $10. What is the maximum assembly floor time that the process can take before it is deemed too expensive to use?

Answer:

(a) 633.3 should be produced manually, 333.3 should be produced semiautomatically, and 33.3 produced robotically, for an average cost of $7.383/toaster.

(b) It can increase by $0.50.

(c) Value is $0.16/minute, willing to purchase 500 at that price.

(d) Objective will go down by 50(10.833).

(e) Cost of $10 versus marginal cost of $10.833, leave 0.83. Unskilled labor costs $0.0833/unit. Therefore, if the new process takes any time at all, it will be deemed too expensive.

1. Only 10 acres of land is suitable for shops.
2. Zoning regulations require at least 1000 trees in the park. A food acre has 30 trees; a ride acre has 20 trees; while a shop acre has no trees.
3. No more than 200 people can work in the park. It takes 3 people to work an acre of rides, 6 to work an acre of food, and 5 to work an acre of shops.

The resulting linear program and Solver output is attached:

 MAX     150 RIDE + 200 FOOD + 300 SHOP
 SUBJECT TO
        RIDE + FOOD + SHOP <=   50
        SHOP <=   10
        20 RIDE + 30 FOOD >=   1000
        3 RIDE + 6 FOOD + 5 SHOP <=   200

-------------------------------------------------------------------

Answer report:

Target Cell (Max)                            
       Cell       Name       Original Value       Final Value
       $B$5       Cost       0                    9062.5

Adjustable Cells                            
       Cell       Name       Original Value       Final Value
       $B$1       Ride       0                    31.25
       $B$2       Food       0                    12.5
       $B$3       Shop       0                    6.25

Constraints                                          
       Cell       Name       Cell Value       Formula       Status       Slack
       $B$6       Land       50               $B$6<=$D$6    Binding      0
       $B$7       ShopLim    6.25             $B$7<=$D$7    Not Binding  3.75
       $B$8       Trees      1000             $B$8>=$D$8    Binding      0
       $B$9       Workers    200              $B$9<=$D$9    Binding      0
 
-----------------------------------------------------------------------------

Sensitivity report:


Adjustable Cells							
                Final      Reduced      Objective      Allowable     Allowable
  Cell  Name    Value      Cost         Coefficient    Increase      Decrease
  $B$1  Ride    31.25      0            150            83.33333333   76.6666667
  $B$2  Food    12.5       0            200            115           125
  $B$3  Shop    6.25       0            300            1E+30         116.666667

Constraints              
                Final  Shadow  Constraint  Allowable  Allowable
  Cell  Name    Value  Price   R.H. Side   Increase   Decrease
  $B$6  Land    50     143.75  50          10         16.66666667
  $B$7  ShopLim 6.25   0       10          1E+30      3.75
  $B$8  Trees   1000  -4.375   1000        166.66667  100
  $B$9  Workers 200   31.25    200         30         50

For each of the following changes, either find the answer or state that the information is not available from the Solver output. In the latter case, state why not.

(a) What is the optimal allocation of the space? What is the profit/hour of the park?

Optimal Allocation: Profit/hour:

(b) Suppose Food only made a profit of $180/hour. What would be the optimal allocation of the park, and what would be the profit/hour of the park?

Optimal Allocation: Profit/hour:

(c) City Council wants to increase our tree requirement to 1020. How much will that cost us (in $/hour). What if they increased the tree requirement to 1200?

Increase to 1020: Increase to 1200:

(d) A construction firm is willing to convert 5 acres of land to make it suitable for shops. How much should Kennytrail be willing to pay for this conversion (in $/hour).

Maximum payment:

(e) Kennytrail is considering putting in a waterslide. Each acre of waterslide can have 2 trees and requires 4 workers. What profit/hour will the waterslide have to generate for them to consider adding it?

Minimum Profit: Reason:

(f) An adjacent parcel of land has become available. It is five acres in size. The owner wants to share in our profits. How much $/hour is Kennytrail willing to pay?

Maximum payment:

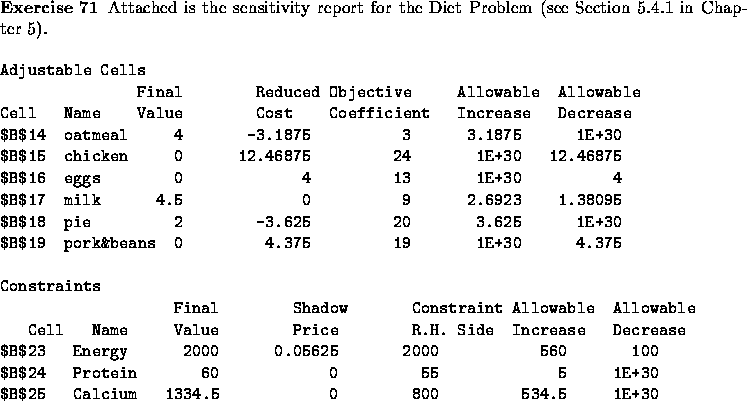
Answer each of the following questions independently of the others.

1. What does the optimal diet consist of?
2. If the cost of oatmeal doubled to 6 cents/serving, should it be removed from the diet?
3. If the cost of chicken went down to half its current price, should it be added to the diet?
4. At what price would eggs start entering the diet?
5. In what range can the price of milk vary (rounding to the nearest tenth of a cent) while the current diet still remaining optimal?
6. During midterms, you need a daily diet with energy content increased from 2000 kcal to 2200 kcal. What is the resulting additional cost?
7. Your doctor recommends that you increase the calcium requirement in your diet from 800 mg to 1200 mg. What is the effect on total cost?
8. Potatoes cost 12 cents/serving and have energy content of 300 kcal per serving, but no protein nor calcium content. Should they be part of the diet?

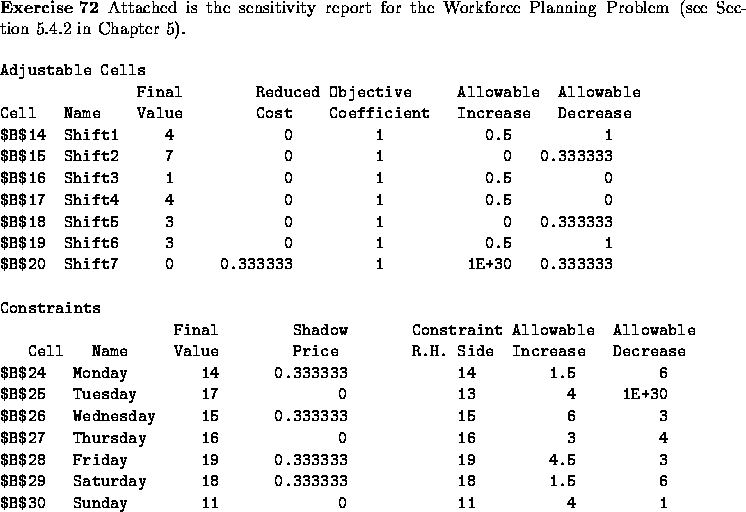
Answer each of the following questions independently of the others.

1. What is the current total number of workers needed to staff the restaurant?
2. Due to a special offer, demand on thurdays increases. As a result, 18 workers are needed instead of 16. What is the effect on the total number of workers needed to staff the restaurant?
3. Assume that demand on mondays decreases: 11 workers are needed instead of 14. What is the effect on the total number of workers needed to staff the restaurant?
4. Currently, 15 workers are needed on wednesdays. In what range can this number vary without changing the optimal basis?
5. Currently, every worker in the restaurant is paid $1000 per month. So the objective function in the formulation can be viewed as total wage expenses (in thousand dollars). Workers have complained that Shift 4 is the least desirable shift. Management is considering increasing the wages of workers on Shift 4 to $1100. Would this change the optimal solution? What would be the effect on total wage expenses?
6. Shift 1, on the other hand, is very desirable (sundays off while on duty fridays and saturdays, which are the best days for tips). Management is considering reducing the wages of workers on Shift 1 to $ 900 per month. Would this change the optimal solution? What would be the effect on total wage expenses?
7. Management is considering introducing a new shift with the days off on tuesdays and sundays. Because these days are not consecutive, the wages will be $ 1200 per month. Will this increase or reduce the total wage expenses?