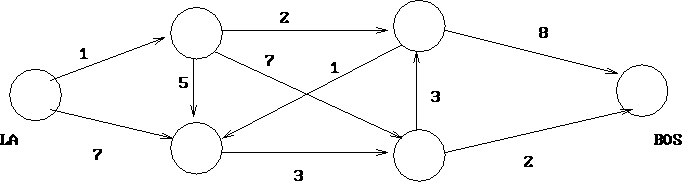
Figure 11.2: Distribution Network
Another type of model again has a number on each arc, but now the number corresponds to a capacity. This limits the flow on the arc to be no more than that value. For instance, in a distribution system, the capacity might be the limit on the amount of material (in tons, say) that can go over a particular distribution channel. We would then be concerned with the capcity of the network: how much can be sent from a source node to the destination node? Using the same network as above, treating the numbers as capacities, how much can be sent from LA to Boston?

Figure 11.2: Distribution Network
Associated with the maximum flow is a bottleneck: a set of arcs whose total capacity equals the maximum flow, and whose removal leaves no path from source to destination in the network. It is actually a nontrivial result to show that the maximum flow equals the size of the minimum bottleneck. It is also an interesting task to find the bottleneck in the above example.
Maximum flow models occur in applications where cost is not an issue, and the goal is to maximize the number of items handled (in a broad sense). Here is a similar problem that can be formulated as a maximum flow problem (this was part of a conversation with a Chicago consulting firm on how to improve their internal operations):
Over the next three months, there are four projects to be completed. Project A requires 8 person-months of work, and must be done by the end of the second month. Project B requires 3 person-months and must be done by end of the first month. Project C can start at the beginning of the second month, and requires 7 person-months of work, no more than 2 of which are in the second month. Project D requires 6 person-months, no more than 3 of which occur in any month. There are 9 consultants available in the first and second month, and 6 in the third. Is it possible to meet the project deadlines? Surprisingly, this is a maximum flow problem. One nice (and surprising) aspect of the result is that this shows that no consultant need split a month's work between jobs.
Figure 11.3: Solution of the exercise.