Unifying Model: Minimum Cost Network Flows

All of the above models are special types of network flow problems: they each have a specialized algorithm that can find solutions hundreds of times faster than plain linear programming.

They can all also be seen as examples of a much broader model, the minimum cost network flow model. This model represents the broadest class of problem that can be solved much faster than linear programming while still retaining such nice properties as integrality of solution and appeal of concept.

Like the maximum flow problem, it considers flows in networks with capacities. Like the shortest path problem, it considers a cost for flow through an arc. Like the transportation problem, it allows multiple sources and destinations. In fact, all of these problems can be seen as special cases of the minimum cost flow problem.

Consider a directed network with n nodes. The decision variables are , the flow through arc (i,j). The given information includes:

• : cost per unit of flow from i to j (may be negative),
• : capacity (or upper bound) on flow from i to j,
• : net flow generated at i.

This last value has a sign convention:

• if i is a supply node,
• if i is a demand node,
• if i is a transshipment node.

The objective is to minimize the total cost of sending the supply through the network to satisfy the demand.

Note that for this model, it is not necessary that every arc exists. We will use the convention that summations are only taken over arcs that exist. The linear programming formulation for this problem is:

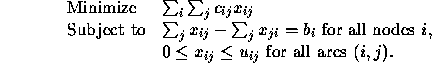
Again, we will assume that the network is balanced, so , since dummies can be added as needed. We also still have a nice integrality property. If all the and are integral, then the resulting solution to the linear program is also integral.

Minimum cost network flows are solved by a variation of the simplex algorithm and can be solved more than 100 times faster than equivalently sized linear programs. From a modeling point of view, it is most important to know the sort of things that can and cannot be modeled in a single network flow problem:

Can do

1. Lower bounds on arcs. If a variable has a lower bound of , upper bound of , and cost of , change the problem as follows:
   • Replace the upper bound with ,
   • Replace the supply at i with ,
   • Replace the supply at j with ,
   Now you have a minimum cost flow problem. Add to the objective after solving and to the flow on arc (i,j) to obtain a solution of the original problem.
2. Upper bounds on flow through a node. Replace the node i with nodes i' and i''. Create an arc from i' to i'' with the appropriate capacity, and cost 0. Replace every arc (j,i) with one from j to i' and every arc (i,j) with one from i'' to j. Lower bounds can also be handled this way.
3. Convex, piecewise linear costs on arc flows (for minimization). This is handled by introducing multiple arcs between the nodes, one for each portion of the piecewise linear function. The convexity will assure that costs are handled correctly in an optimal solution.

Can't do

1. Fixed cost to use a node.
2. Fixed cost to use an arc.
3. ``Proportionality of flow.'' That is, if one unit enters node i, then you insist that .5 units go to node j and .5 to node k.
4. Gains and losses of flow along arcs, as in power distribution.

Note that although these cannot be done in a single network, it may be possible to use the solutions to multiple networks to give you an answer. For instance, if there is only one arc with a fixed cost, you can solve both with and without the arc to see if it is advantageous to pay the fixed cost.