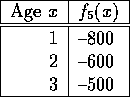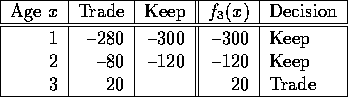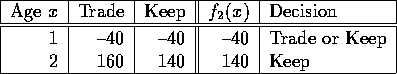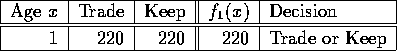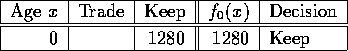Equipment Replacement

In the network homework, you already saw how to formulate and solve an equipment replacement problem using a shortest path algorithm. Let's look at an alternative dynamic programming formulation.

Suppose a shop needs to have a certain machine over the next five year period. Each new machine costs $1000. The cost of maintaining the machine during its ith year of operation is as follows: , , and . A machine may be kept up to three years before being traded in. The trade in value after i years is , , and . How can the shop minimize costs over the five year period?

Let the stages correspond to each year. The state is the age of the machine for that year. The decisions are whether to keep the machine or trade it in for a new one. Let be the minimum cost incurred from time t to time 5, given the machine is x years old in time t.

Since we have to trade in at time 5,

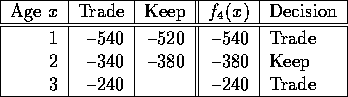
Now consider other time periods. If you have a three year old machine in time t, you must trade in, so

If you have a two year old machine, you can either trade or keep.

• Trade costs you .
• Keep costs you .

So the best thing to do with a two year old machine is the minimum of the two.

Similarly

Finally, at time zero, we have to buy, so

This is solved with backwards recursion as follows:

Stage 5.

Stage 4.

Stage 3.

Stage 2.

Stage 1.

Stage 0.

So the cost is 1280, and one solution is to trade in years 1 and 2. There are other optimal solutions.