Linear programming is a wonderful technique, particularly for modelling. In fact, it is very easy to create models for problems that can't be solved, nor will they be solved with any conceivable advance in computer technology. This can be rather disheartening Here is this wonderful model, but we can't solve it. In this section of the course, we will be looking at a powerful method for solving large linear programs: decomposition. We start with the problem of how to solve linear programs with many, many, variables. To fix ideas, let's begin with a very simple linear program for capital budgeting.
Pension funds, banks and other institutions with an excess of cash laying around are continually faced with the problem of investing the money in suitable stocks, bonds, and other financial instruments. This also occurs on a smaller scale. Consider a lawsuit where the plaintiff has won an award for future medical expenses. The defendant must crate a lump sum sufficient to provide an annual payment to cover the award. Naturally, the defendant would like this lump sum to be as small as possible while still meeting the court-mandated expenses. Using linear programming, it is possible to minimize the lump sum while meeting various restrictions on the investments.
Let us begin with a much simpler portfolio selection problem, taken from Shapiro. Here there is a certain amount to be invested, with five possible bonds to invest in. There are restrictions on how the money can be invested (restrictions on risk, on length of time until maturity, on municipal investments), but all this leads to a fairly standard linear programming formulation.
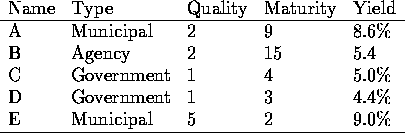
The data for this problem is as follows:
There are five bonds. Each has a type, a quality rating (1 is best), a number of years to maturity, and a yield. The objective is to maximize the average yield, subject to the following constraints:
There are a number of other restrictions that can be added to this model. For more information, see the article by Cohen and Hammer in Optimization models for strategic planning.
This leads to the linear program:
Maximize 
Subject to
(Don't worry if this is not immediately obvious: it takes some work to get here.)
There are a number of different objective functions possible. One might be to maximize the net present value of the investments. Another might be to maximize the average internal rate of return. A third (as in the lawsuit) is to minimize the outlay required to meet the restrictions.
So far, we have just a simple linear program. Trying to implement it, however, is another matter. There are thousands of bonds available. If you include all the stocks, futures, and other investment opportunities, the number of variables grows into the hundreds of thousands. Furthermore, these decisions would be made very often (ideally with every customer inquiry), further limiting the time available.
Of course, people make these decisions all the time. Let's step back and see how we can do this by hand.
Suppose risk is measured from 1 to 10 (most risky) and I have placed an upper bound of 5 on the average risk. Suppose further that my current investment portfolio has an average risk of 3 and return of 1.10. Clearly, I would like to find an investment with better return and more risk to balance my portfolio. For instance, an investment with return 1.25 and risk 8 might be added. But suppose it is a municipal bond and I am at my limit for municipal investment. Should I still add this investment?
In general, we would look for investments that help us where we are weak and hurt us where we are strong. It is doing the tradeoffs that is the hard part.
Surprisingly, we can implement this approach formally. The dual variables contain all the information we need. The dual values tell us how to do the tradeoffs.
Here is the linear programming output from LINDO for this problem.
MAX 0.086 XA + 0.054 XB + 0.05 XC + 0.044 XD + 0.09 XE
SUBJECT TO
2) XA + XB + XC + XD + XE <= 10
3) XA + XE <= 3
4) 0.6 XA + 0.6 XB - 0.4 XC - 0.4 XD + 3.6 XE <= 0
5) 4 XA + 10 XB - XC - 2 XD - 3 XE <= 0
END
LP OPTIMUM FOUND AT STEP 3
OBJECTIVE FUNCTION VALUE
1) 0.59672731
VARIABLE VALUE REDUCED COST
XA 2.181818 0.000000
XB 0.000000 0.060364
XC 7.363636 0.000000
XD 0.000000 0.001273
XE 0.454545 0.000000
ROW SLACK OR SURPLUS DUAL PRICES
2) 0.000000 0.059673
3) 0.363636 0.000000
4) 0.000000 0.012364
5) 0.000000 0.004727
BRIEF REVIEW
There are many numbers in the output. In this section, we need a firm understanding of the dual prices (I am really spending this section showing you how useful dual prices are). The dual price is an approximation of the value of changing the right hand side of the corresponding constraint by 1. For instance, increasing the money available to $11 million is equivalent to changing the right hand side of row 2 (the objective is row 1) from 10 to 11. This is an increase of 1, so the objective will increase by approximately .059673. Similarly, if we decreased the right hand side of constraint 5 to -2, the objective would decrease by approximately 2(.004727)=.009454. If we similtaneously increased the right hand side of row 2 by 1 and decreased the right hand side of row 5 by 2, the objective would go up by approximately .059673-.009454=.050219.
At the moment, that is all I need you to recall from your OR class.
In this example, the optimal solution has
= 2.18, 
= 7.36, 
= .46, with value .597
The duals are 0.06, 0.0, 0.012, and 0.005 (corresponding to the four constraints above).
Now suppose we have a municipal bond with return .07, quality 2, maturity 4 years. If we forced ourselves to buy $1 million of this bond, how would the linear program change? Well, the amount available for the other bonds would be $9 million (so that constraint would have its right hand side decreased by 1); the municipal limit would become a 2 (so that right hand side decreases by 1); the quality constraint right hand side decreases by .6; and the maturity constraint's right hand side increases by 1. The overall effect of this is to change the objective by
The objective goes down by .062. But we have forced ourselves to own $1 million of the bond, so that gives us .07 in the objective. The net gain is an improvement of .008. We are better off buying this new bond.
This calculation is called the reduced cost calculation. It calculates the cost of the bond relative to the current solution. In general, we will want ``good'' variables to have a negative cost, and bad ones to have a positive cost, so we would write the above calculation as
-.07+1(.06)+1(0.0)+.6(0.012)+(-1)(0.005) = -.0078.
If the quality had been a 3, then the reduced cost would have been .0042 and the investment would not have been considered.
In general, let c be the objective function coefficient of an
investment under consideration and let 
be the coefficient of the
investment in the ith constraint. Let 
be the dual value
corresponding to the ith constraint. Calculate
and add the investment to the portfolio only if this value is negative.
We can use this insight to create a process called variable generation. Begin with a small number of variables and solve the restricted linear program. Then determine if any variable not included is eligible to enter the basis. If so, add it to the set under consideration and repeat. Otherwise, stop, you have the optimal solution over all the variables.
The advantage of this approach is that most of the data never enters the linear programming package at all: it can remain in the spreadsheet, or database, or wherever it is. All that is required is the ability to calculate a reduced cost, a straightforward operation for every spreadsheet and database.