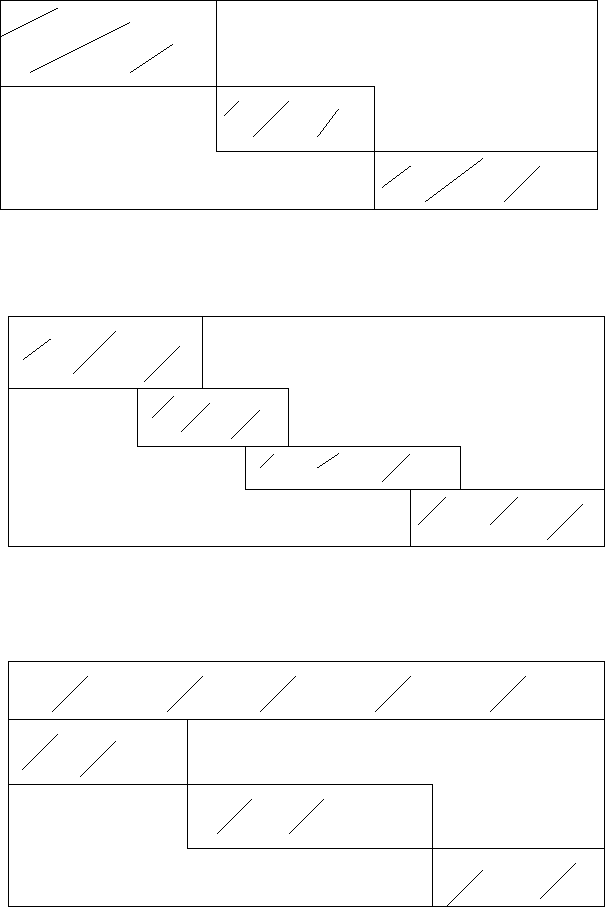
Figure .1: Problem Types
Current linear programming codes are able to solve linear programs with perhaps 10,000 rows and 50,000 columns routinely. Larger problems can be solved if special care is made to avoid round-off errors and other numerical difficulties. Many models create linear programs that are far larger than this, however. For instance, the oil industry creates enormous models involving purchasing, shipping, and blending. Most of these models are expanded over time, so instead of just a variable for, say, the amount of jet fuel produced at a certain facility, the variable is for the amount of jet fuel produced at a certain facility on a given day. It is clear that the model can get very quick, very fast.
Fortunately, models this large have a lot of internal structure. For instance, it is very rare to find very large models where the nonzeros in the constraint matrix are more than .1% of the total. Therefore, most linear programs contain a tremendous number of 0s. Furthermore, if we plot where the 0s are, many models fall into a limited number of patterns, as shown in the figure.
If the problem is independent, then each piece can be solved on its own. In fact, all facets of the O.R. process can be done on each individual piece: data collection, model verification, solution, sensitivity analysis and so on. By the way, linear programming packages solve a number of individual pieces much faster than the linear program consisting of all of them.
We will concentrate on block angular systems. Similar methods hold for staircase and other large scale, structured systems.
Block angular systems consist of some common rows which contain nearly all the variables. The remaining rows are divided into sets with corresponding variables that are contained in the rows. Each variable is in exactly one set. These sets define subproblems.
To solve this sort of linear program, we create one master problem. The master problem will handle the common constraints by asking the subproblems for proposals. The master problem will choose a combination of proposals that maximizes profits while meeting the common constraints.
In general, the master problem will assign variables ![]() for
the jth proposal from the ith subproblem. The common constraints
are written in terms of these
for
the jth proposal from the ith subproblem. The common constraints
are written in terms of these ![]() s to give the linear program:
s to give the linear program:
Maximize (profit in terms of ![]() )
)
Subject to
(common constraints in terms of ![]() )
)
![]() for all i
for all i
![]() for all i and j
for all i and j
Let's assume we have an initial set of proposals so that the above linear program has a feasible solution. The above linear program states only that it wants to choose a combination of proposals so as to meet the constraints and maximize profit. Once we have this proposal, we simply do variable generation. In other words, we find the shadow prices (or dual values), and ask for proposals from each subproblem. We add the proposals to the master problem, and resolve. We terminate when every subproblem gives a proposal that is already in the master problem.
In the previous example, the common constraint was on . There were two subproblems, corresponding to each division.
To illustrate the mechanics of this method, here is another example.
Maximize ![]()
Subject to
![]()
![]()
![]()
![]()
![]()
In this case (like most) we have a number of possibilities for common
constraints, subproblems and so on. For a change, let's put the 1st
and 3rd constraint as the common constraints, and the 2nd and 4th as
the subproblem (one subproblem is o.k.) with variables ![]() and
and
![]() . Note that
. Note that ![]() is only in the master problem, not in any
subproblem. An initial proposal is to have
is only in the master problem, not in any
subproblem. An initial proposal is to have ![]() .
Calling this
.
Calling this ![]() , this gives us the master problem (I will assume
non-negativity is included in all formulations):
, this gives us the master problem (I will assume
non-negativity is included in all formulations):
Maximize ![]()
Subject to
![]()
![]()
![]()
Notice that ![]() has very little effect. The optimal solution to
this is
has very little effect. The optimal solution to
this is ![]() with value 21. The dual of the first
constraint is 0. The subproblem to solve is then:
with value 21. The dual of the first
constraint is 0. The subproblem to solve is then:
Maximize ![]()
Subject to
![]()
![]()
The solution to this (and hence the proposal to the master problem) is
![]() . We will now place this proposal in the master
problem as
. We will now place this proposal in the master
problem as ![]() . This proposal uses 8 units in constraint 1, and
has profit 21, so the master is:
. This proposal uses 8 units in constraint 1, and
has profit 21, so the master is:
Maximize ![]()
Subject to
![]()
![]()
![]()
The optimal solution to this is ![]() ,
with value 39.4. The dual to the first constraint is 21/8. We can
therefore update the costs in the subproblem to be 5-2(21/8) for
,
with value 39.4. The dual to the first constraint is 21/8. We can
therefore update the costs in the subproblem to be 5-2(21/8) for ![]() and 3-21/8 for
and 3-21/8 for ![]() . Now the subproblem is:
. Now the subproblem is:
Maximize ![]()
Subject to
![]()
![]()
The proposal generated is ![]() . Again, this is added to
the master program as
. Again, this is added to
the master program as ![]() . It's profit is 15, and its use in
constraint 1 is 5. The master is now:
. It's profit is 15, and its use in
constraint 1 is 5. The master is now:
Maximize ![]()
Subject to
![]()
![]()
![]()
You can now go out and continue this example on your own.
At this point, you should be getting some sort of feel for these sorts of problems. The essential idea is to request proposals from the subproblems, using the dual values to price resources so that the resulting proposals are good for the overall problem.
This sort of decomposition is very often used. Some of the advantages:
Practically, the main drawback of this approach is in possible convergence problems. Normally, this method gets very good answers quickly, but it requires a lot of time to find the optimal solution. The subproblems may continue to generate proposals only slightly better than the ones before.
Despite this problem, this sort of decomposition is a necessity whenever a large, structured linear program requires solving.