We have already covered the basic idea about when to use heuristics: when time or other limitations prohibit the finding of optimal solutions. Until you have a fair amount of experience in implementing optimization and heuristic computer codes, however, this may be a bit vague. There is one class of problems that can be identified (sometimes easily) for which the following is known: the best solution technique you are likely to find is to search all solutions (perhaps with branch and bound to help). In this case, if the problems are anything except tiny, solutions can not be reliably found in a reasonable amount of time. This class is known as the NP-complete problems.
Before we get into the details, let me tell you a story. Back in Canada, I was working for a consulting firm (a small one of three people) who did a lot of work in nurse scheduling for hospitals. Nurse scheduling is one of those ``Gee, I wish we didn't have to do this'' sort of jobs where a lot of money is tied up. My boss (a professor) had some very good ideas about how to schedule nurses (who are very difficult to schedule due to varying abilities, union and seniority rules, and varying work loads). I was working on some smaller pieces for him.
One piece was as follows: there are a number of shifts (like 9-5, 8-5, 8-12, 10-2, and so on) and a varying requirement over the day (perhaps 10 nurses from 10-11, 12 nurses from 11-12, and so on). The problem was to determine how many nurses to assign to each shift to minimize the cost of the nurses used (due to various restrictions, not every shift was possible, and not every shift had the same cost per hour). How could we solve this?
Knowing a bit about heuristics back then, I went to work on various heuristics for this problem. I could see no obvious algorithm, so it seemed that I was doing the right thing.
A few weeks later, I was leafing through an issue of Operations Research, where I saw a paper by John Bartholdi (together with Don Ratlif, who later became my dissertation advisors). In this paper, he pointed out that this scheduling problem is really a ``disguised'' network problem. The details are not important. The important aspect is that I could solve all these problems exactly very quickly with network techniques.
How could I have recognized that I did not need to go to heuristics. Conversely, how can I recognize when I need to go to heuristics and branch and bound? Herein lies the theory of NP-completeness.
All the ``good'' algorithms I have presented in this course are polynomial in the size of the input (say the number of nodes and edges). Conversely, I have avoided exponential algorithms every step of the way. This polynomial, non-polynomial divide is considered the fundamental divide. Problems with polynomial solution algorithms are called easy while those without known polynomial solution algorithms are called hard.
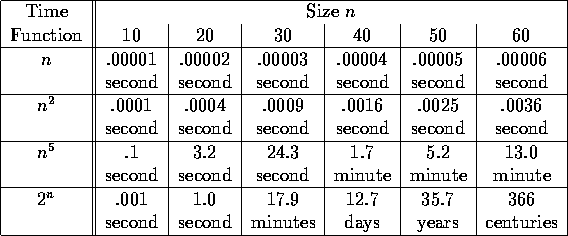
Why do we use this divide? Consider what happens as problems get bigger. If we let n be the size of an instance and let the following function represent time needed in microseconds, let's see how different functions work:
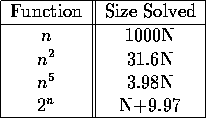
Another way to see this is to suppose that suddenly a much faster computer appears on the scene, say 1000 times faster than the one you are currently using. Suppose you can currently solve a problem of size N. How large a problem can you solve now? The following table shows some interesting differences:
The distinction seems very important.
Some examples of problems with polynomial solution algorithms are:
Minimum cost flow
Maximum flow
Minimum spanning tree
Linear programming
Canadian traveling salesman problem
Some examples of those without known polynomial solution algorithms are:
Integer programming
Knapsack problem
Traveling salesman problem with arbitrary distances
Satisfiability
What is needed is a mechanism for deciding which class a given problem falls in.
The theory revolves around the following fact: there are a large number of problems that are not known to have polynomial solution methods. These problems have the following nice property: if one of them has a polynomial time solution method, then they all do. In other words, if one of them is easy, then they all are. A lot of very, very bright people have tried to find polynomial solution methods for these problems and have failed. Therefore, it is likely that there do not exist any such methods (or, to be blunter, it is unlikely that you or I will find one). So if we determine that our problem is a member of this class of problems, then we can rest assured that no one will find a polynomial algorithm, so we can resort to branch and bound or heuristics.
This class of problems are called the NP-complete problems. (NP stands for nondeterministic polynomial. A problem is in NP if you can verify a solution in polynomial time. The NP-complete problems are the hardest of the NP problems.) All of the examples above of problems with no known solution are NP-complete. How does one go about proving a problem is NP-complete? The main idea is that of reduction. Suppose I want to prove problem P is hard. Let's suppose I also know that problem P' is NP-complete (say by looking it up in Garey and Johnson's book). If I can write any instance of P' as an instance of P, then I will also know that P is NP-complete.
For instance, suppose I knew that the TSP is NP-complete and I was
faced with the problem of the giving an algorithm for the following:
Given a graph G with costs on the edges, and integer 
for each
node i, find a
minimum cost spanning tree such that no node is incident to more than
edges. Call this problem the Restricted Minimum Spanning Tree
Problem (RMST).
You can determine that this problem is NP-complete as follows:
suppose you have a method to solve RMST for any graph and any k.
Then, solve the traveling salesman problem as follows: Take any node
(say node A) and divide it into two nodes A' and A''. Attach both
A' and A'' to all nodes A was attached to with the cost on each
edge the same as in the original graph. Set 
and 
to
be 1 and to be 2 for all other nodes. Now solve this RMST. It
is clear that this gives a solution to the TSP. Therefore, if you can
solve RMST, you can solve the TSP. Since thousands have worked on the
TSP, it is unlikely you can solve RMST.
Note the direction of proof: you must start with the known hard problem and write it in terms of the unknown problem. DON'T DO THE REVERSE.
There are a few technical restrictions. For instance, the size of the transformed problem must not be too much larger than the size of the original problem (within a polynomial factor).
Note that sometimes easy and hard problems seem very similar. For instance, shortest path (with nonnegative costs) is easy; longest paths are hard. Minimum spanning tree is easy; minimum spanning tree with limit on arcs per node is hard. It is not until you find algorithms or find an NP-completeness result that you can distinguish the problems.
NP-completeness results can be very clever. By far the most common type of NP-completeness result is of the above type: a problem is hard because it contains a hard problem.
NP-completeness allows you to know when to use heuristics: use it for NP-complete problems, because the best known algorithms essentially examine all solutions. But remember: if you do find a polynomial solution procedure for an NP-complete problem, you will be very, very famous.