One popular (in some circles, extremely popular) general heuristic technique is that of neural networks. If simulated annealing appeals to physicists and genetic algorithms appeal to biologists, neural networks appeal to brain surgeons. By drawing an analogy with how the brain stores and processes information, neural networks attempt to mimic the brain's flexibility in solving problems.
Before I can talk about the brain, let me talk about a single processing unit: a neuron. In this model, a neuron receives input from other neurons and the outside world. The neuron then uses a simple mathematical transformation to give its output. In this model, we will assume that the output of a neuron can be adequately represented by a real value between 0 and 1.
This transformation works as follows: for neuron j, suppose it
takes inputs from neurons 1, 2, ..., n (generically i). Each of
these inputs are values between 0 and 1. For each i, neuron j has
a weight 
. This weight gives a measure of the value j gives
to i's input. If the weight is 0, i will have no effect on j.
If the weight is a high positive number, then j will want to turn on
when i turns on (turning on means to have the value 1). If the
weight is a high negative number, then j will want to turn off when
i turns on. If the inputs have value 
, the total input is then
given the value 
. Since this can be a large
positive or negative value, this must be transformed into the 0-1
range. This is normally done through a sigmoid curve, which is one
that looks as follows:
There are many sigmoid curves. One example is
Note if W is very large (positive) this becomes very close to 1, while if W is very large negative this goes to 0.
A neural network is nothing more than a collection of these neurons connected to each other and to the outside world (both to get data and to provide responses).
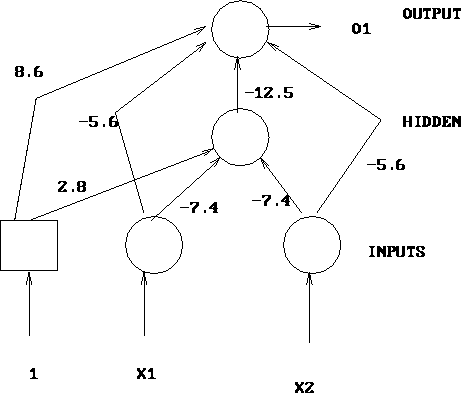
Figure 2: Simple Neural Network
Here there are two inputs and one output. Neuron 3 is
a hidden layer. Neuron 5 is a special neuron that always sends
out a 1. Now, consider what happens when the inputs are 1 and 0,
respectively. The input to 3 is 2.8-7.4, so the output is
or 0.01. This gives the input to node 4 to be
8.6-5.6-12.5(.01) = 2.876, so the output is 
or .947. If we treat all numbers over .9 as 1 and those less than .1
as 0 (and all others inconclusive), we can treat that output as a 1.
If the inputs are restricted to be 0 or 1, this network models the
following function:
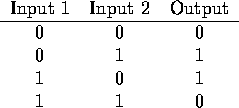
Now this network may not look too exciting, but this network (or, more precisely, the automatic generation of this network) signified the beginning of neural networks as a practical computing technique.
There are two fundamentally different ways of using neural networks: the first is to assign weights and connections to enforce constraints and optimization goals and then see if the network ``settles down'' into a good (or optimal) solution. For instance, for the traveling salesman problem, it is possible to create a neural network in a grid, where the i,j neuron corresponds to visiting city i in the jth position. Now, negative weights (inhibitors) must be assigned so that no two cities are placed in the same position. Positive weights (excitors) are placed between cities that are close to each other to encourage placing them one after another in the circuit. Once all the weights are decided on, a random set of values is placed in the network and those values are updated until it reaches a steady state. This is then a solution (or not, depending on the exact result).
This approach has not been terrifically successful to date. For most structured problems, it is tremendously difficult to enforce feasibility requirements in such a way that doesn't totally overwhelm the optimality requirements.
The second approach has been much more successful in many domains. In this case, an unstructured neural net is trained to give a good response. The easiest way to see this is to imagine the neural net as a black box attempting to mimic some unknown function. The function maps the inputs into the output(s). Now assume you have a tremendous amount of past data giving the inputs and the ``correct'' output. Beginning with a ``random'' neural net, you can feed the first input in and observe the response. If the response is wrong, you can change the weights along the paths that generated that response. You can also use the correct response to change the weights to generate the correct response. Once you do this for a few thousand data points, it is likely that your black box is mimicking the function reasonably well (at least along the dimensions of your original data).
Of course, all this can be done automatically. There are many learning algorithms that have been developed (the big breakthrough was the learning algorithm and insight into the minimal requirements of the structure that lead to the network used above). These algorithms work quickly and accurately to train small to medium neural networks (say up to 50 neurons). These networks have been and are being used in many applications. Here are a few:
In all these applications and many more, neural networks have proven to be more robust and accurate than any regression or other mathematical modeling tool.
Currently, I would say that a neural network approach is very appealing for many applications involving either the classification or the prediction of a system. It has been less successful to date in the optimization of systems.
