Suppose we wish to invest $14,000. We have identified four investment opportunities. Investment 1 requires an investment of $5,000 and has a present value (a time-discounted value) of $8,000; investment 2 requires $7,000 and has a value of $11,000; investment 3 requires $4,000 and has a value of $6,000; and investment 4 requires $3,000 and has a value of $4,000. Into which investments should we place our money so as to maximize our total present value?
As in linear programming, our first step is to decide on our
variables. This can be much more difficult in integer programming
because there are very clever ways to use integrality restrictions.
In this case, we will use a 0-1 variable 
for each investment.
If is 1 then we will make investment j. If it is 0, we will
not make the investment. This leads to the 0-1 programming problem:
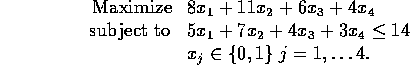
Now, a straightforward ``bang for buck'' suggests that investment 1 is
the best choice. In fact, ignoring integrality constraints, the
optimal linear programming solution is 
, 
, 
, 
for a value of $22,000. Unfortunately, this solution
is not integral. Rounding 
down to 0 gives a feasible solution
with a value of $19,000. There is a better integer solution,
however, of 
, 
for a value of $21,000.
This example shows that rounding does not necessarily give an optimal
value.
There are a number of additional constraints we might want to add. For instance, consider the following constraints:
All of these, and many more logical restrictions, can be enforced using 0-1 variables. In these cases, the constraints are:
.
