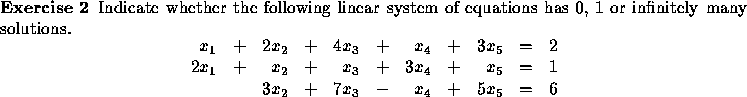The Gauss-Jordan elimination procedure is a systematic method for solving systems of linear equations. It works one variable at a time, eliminating it in all rows but one, and then moves on to the next variable. We illustrate the procedure on three examples.
Another example:
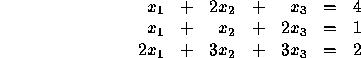
First we eliminate ![]() from equations 2 and 3.
from equations 2 and 3.
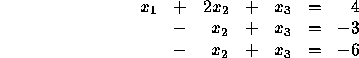
Then we eliminate ![]() from equations 1 and 3.
from equations 1 and 3.
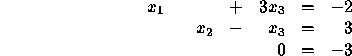
Equation 3 shows that the linear system has no solution.
A third example:
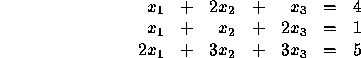
Doing the same as above, we end up with
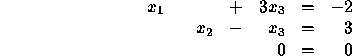
Now equation 3 is an obvious equality. It can be discarded to obtain
![]()
The situation where we can express some of the variables (here ![]() and
and ![]() ) in terms of the remaining variables (here
) in terms of the remaining variables (here ![]() ) is
important. These variables are said to be basic and
nonbasic respectively.
Any choice of the nonbasic variable
) is
important. These variables are said to be basic and
nonbasic respectively.
Any choice of the nonbasic variable ![]() yields a solution of
the linear system. Therefore the system has infinitely many
solutions.
yields a solution of
the linear system. Therefore the system has infinitely many
solutions.