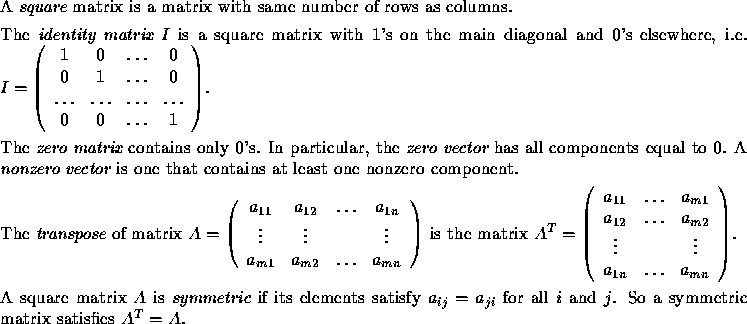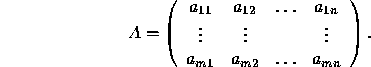
It is useful to formalize the operations on vectors and matrices that form the basis of linear algebra. For our purpose, the most useful definitions are the following.
A matrix is a rectangular array of numbers written in the form
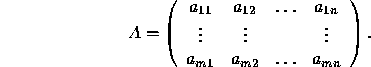
The matrix A has dimensions ![]() if it has m rows
and n columns. When m=1, the matrix is called a row vector;
when n=1, the matrix is called a column vector. A vector
can be represented either by a row vector or a column vector.
if it has m rows
and n columns. When m=1, the matrix is called a row vector;
when n=1, the matrix is called a column vector. A vector
can be represented either by a row vector or a column vector.
Equality of two matrices of same dimensions:
Let 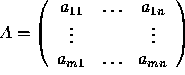 and
and 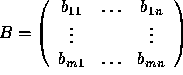 .
.
Then A=B means that ![]() for all i,j.
for all i,j.
Multiplication of a matrix A by a scalar k:
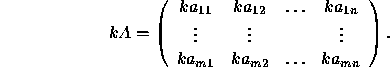
Addition of two matrices of same dimensions:
Let 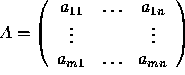 and
and 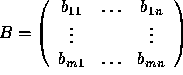 .
.
Then
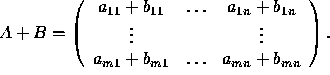
Note that A+B is not defined when A and B have different dimensions.
![]()
Multiplication of a matrix of dimensions ![]() by
a matrix of dimensions
by
a matrix of dimensions ![]() :
:
Let 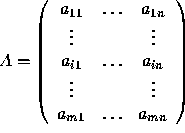 and
and 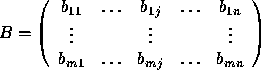 .
.
Then AB is a matrix of dimensions ![]() computed as follows.
computed as follows.
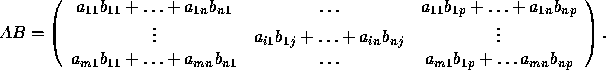
As an example, let us multiply the matrices

The result is 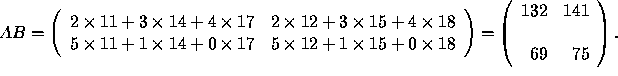
Note that AB is defined only when the number of columns of A equals the number of rows of B. An important remark: even when both AB and BA are defined, the results are usually different. A property of matrix multiplication is the following:
![]()
That is, if you have three matrices A, B, C to multiply and the product is legal (the number of columns of A equals the number of rows of B and the number of columns of B equals the number of rows of C), then you have two possibilities: you can first compute AB and multiply the result by C, or you can first compute BC and multiply A by the result.

Remark: A system of linear equations can be written conveniently using matrix notation. Namely,

can be written as

or as
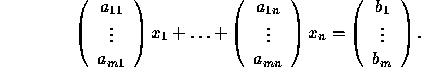
So a matrix equation Ax = b where A is a given ![]() matrix,
b is a given m-column vector and x is an unknown n-column vector,
is a linear system of m equations in n variables. Similarly, a vector
equation
matrix,
b is a given m-column vector and x is an unknown n-column vector,
is a linear system of m equations in n variables. Similarly, a vector
equation ![]() where
where ![]() are given
m-column vectors and
are given
m-column vectors and ![]() are n unknown real numbers,
is also a system of m equations in n variables.
are n unknown real numbers,
is also a system of m equations in n variables.
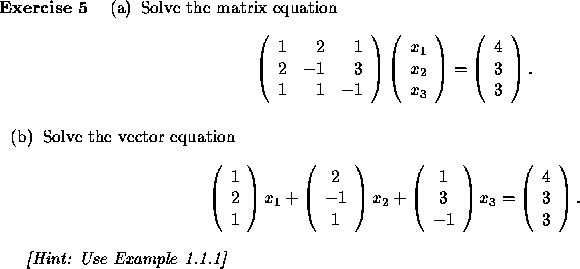
The following standard definitions will be useful: