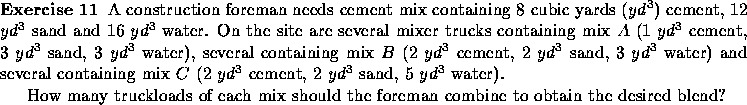Suppose
that the vector (1,3) represents the contents of a ``Regular'' can of
mixed nuts (1 lb cashews and 3 lb peanuts) while (1,1) represents a
``Deluxe'' can (1 lb cashews and 1 lb peanuts). Can you
obtain a mixture of 2 lb cashews and 3 lb peanuts by combining the two
mixtures in appropriate amounts?
The answer is to use ![]() cans of Regular and
cans of Regular and ![]() cans of
Deluxe in order to satisfy the equality
cans of
Deluxe in order to satisfy the equality
![]()
This is none other than a system of two linear equations:
![]()
The solution of these equations (obtained by the Gauss-Jordan procedure)
is ![]() ,
, ![]() . So
the desired combination is to mix 1/2 can of Regular nuts with 3/2 cans of
Deluxe nuts. Thus if some recipe calls for the mixture (2,3), you can
substitute 1/2 can of Regular mix and 3/2 can of Deluxe mix.
. So
the desired combination is to mix 1/2 can of Regular nuts with 3/2 cans of
Deluxe nuts. Thus if some recipe calls for the mixture (2,3), you can
substitute 1/2 can of Regular mix and 3/2 can of Deluxe mix.
Suppose now that you want to obtain 1 lb cashews and no peanuts. This poses the equations,
![]()
The solution is ![]() . Thus you can obtain a pound of
pure cashews by buying 3/2 cans of Deluxe mix and removing enough nuts to
form 1/2 can Regular mix, which can be sold. In this case
it is physically possible to use a
negative amount of some ingredient, but in other cases it may be
impossible, as when one is mixing paint.
. Thus you can obtain a pound of
pure cashews by buying 3/2 cans of Deluxe mix and removing enough nuts to
form 1/2 can Regular mix, which can be sold. In this case
it is physically possible to use a
negative amount of some ingredient, but in other cases it may be
impossible, as when one is mixing paint.
A vector of the form  is called a linear combination of the vectors
is called a linear combination of the vectors
![]() and
and
![]() .
In particular we just saw that the vector
.
In particular we just saw that the vector
![]() is a linear combination of
the vectors
is a linear combination of
the vectors
![]() and
and
![]() .
And so is
.
And so is
![]() .
.
The question arises: can one obtain any mixture whatever by
taking the appropriate combination of Regular and Deluxe cans?
Is any vector
![]() a linear combination of
a linear combination of
![]() and
and
![]() ?
?
To answer the question, solve the equations in general. You
want a mixture of ![]() lb cashews and
lb cashews and ![]() lb peanuts and set
lb peanuts and set
![]()
or equivalently,
![]()
These equations
have a unique solution, no matter what are the values of ![]() and
and ![]() ,
namely,
,
namely,
![]()
No matter what vector ![]() you want, you can get it as a linear
combination of (1,3) and (1,1). The vectors (1,3) and (1,1) are
said to be linearly independent.
you want, you can get it as a linear
combination of (1,3) and (1,1). The vectors (1,3) and (1,1) are
said to be linearly independent.
Not all pairs of vectors can yield an arbitrary mixture
![]() . For instance, no linear combination of (1,1) and (2,2)
yields (2,3). In other words, the equations
. For instance, no linear combination of (1,1) and (2,2)
yields (2,3). In other words, the equations
![]()
have no solution.
The reason is that (2,2) is already a multiple of (1,1), that is (2,2) is a linear combination of (1,1). The vectors (1,1) and (2,2) are said to be linearly dependent.
If (2,2) represents, for instance, a large Deluxe can of nuts and (1,1) a small one, it is clear that you cannot obtain any mixture you want by combining large and small Deluxe cans. In fact, once you have small cans, the large cans contribute nothing at all to the mixtures you can generate, since you can always substitute two small cans for a large one.
A more interesting example is (1,2,0), (1,0,1) and (2,2,1). The third vector is clearly a linear combination of the other two (it equals their sum). Altogether, these three vectors are said to be linearly dependent. For instance, these three vectors might represent mixtures of nuts as follows:
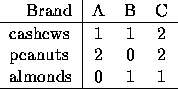
Then once you have brands A and B, brand C adds nothing whatever to the variety of mixtures you can concoct. This is because you can already obtain a can of brand C from brands A and B anyway. In other words, if a recipe calls for brand C, you can always substitute a mixture of 1 can brand A and 1 can brand B.
Suppose you want to obtain the mixture (1,2,1) by combining Brands A, B, and C. The equations are
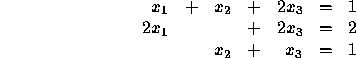
If you try to solve these equations, you will find that there is no solution. So the vector (1,2,1) is not a linear combination of (1,2,0), (1,0,1) and (2,2,1).
The concepts of linear combination, linear dependence and linear independence introduced in the above examples can be defined more formally, for any number of n-component vectors. This is done as follows.
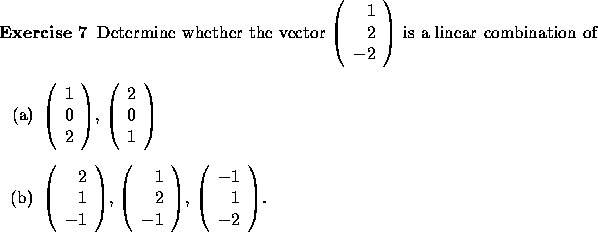
In linear programming, there are typically many more variables than equations. So, this case warrants looking at another example.
This is really a mixing problem. Rather than peanuts and cashews, the mixture will contain leather and labor. The items to be mixed are four activities: manufacturing a deluxe belt, manufacturing a regular belt, leaving a leftover leather strip in inventory, and leaving an hour of labor idle (or for other work). Just as each Regular can of mixed nuts contributes 1 pound of cashews and 3 pounds of peanuts to the mixture, each regular belt will consume 1 leather strip and 2 hours of labor. The aim is to combine the four activities in the right proportion so that 40 strips and 60 hours are accounted for:
![]()
So,
In tableau form, the equations are:= number of deluxe belts made
= number of regular belts made
= number of leather strips left over
= number of labor hours left over
Since there are only two equations, you can only solve for two variables.
Let's solve for ![]() and
and ![]() , using Gauss-Jordan elimination. After
the first iteration you get,
, using Gauss-Jordan elimination. After
the first iteration you get,
A second iteration yields the solution,
This tableau represents the equations
![]()
or,
You can't say how many deluxe belts ![]() and regular belts
and regular belts ![]() the
plant will make until you specify how much leather
the
plant will make until you specify how much leather ![]() and labor
and labor ![]() will be left over. But (1.6) is a formula for computing how
many belts of either type must be made, for any given
will be left over. But (1.6) is a formula for computing how
many belts of either type must be made, for any given ![]() and
and ![]() . So
the equations have many solutions (infinitely many).
. So
the equations have many solutions (infinitely many).
For example, if you want to have nothing left over ( ![]() ), you will
make 20 of each. If you want to have 5 strips and 5 hours left over, you
will make
), you will
make 20 of each. If you want to have 5 strips and 5 hours left over, you
will make ![]() deluxe and
deluxe and ![]() regular belts.
regular belts.
The variables ![]() you solved for are called basic variables.
The other variables are nonbasic. You have control of the nonbasic
variables. Once you give them values, the values of the basic variables
follow. A solution in which you make all the nonbasic variables zero is
called a basic solution.
you solved for are called basic variables.
The other variables are nonbasic. You have control of the nonbasic
variables. Once you give them values, the values of the basic variables
follow. A solution in which you make all the nonbasic variables zero is
called a basic solution.
Can you have basic variables other than ![]() ? Sure. Any pair of
variables can be basic, provided the corresponding columns in
(1.3) are linearly independent (otherwise, you can't solve for
the basic variables).
? Sure. Any pair of
variables can be basic, provided the corresponding columns in
(1.3) are linearly independent (otherwise, you can't solve for
the basic variables).
Equations (1.3), for instance, are already solved
in (1.3) for basic
variables ![]() . Here the two basic activities are having leftover
leather and having leftover labor. The basic solution is
. Here the two basic activities are having leftover
leather and having leftover labor. The basic solution is
![]() . This means that if you decide to produce no belts
(
. This means that if you decide to produce no belts
( ![]() ), you must have 40 leftover leather strips and 60 leftover
labor hours.
), you must have 40 leftover leather strips and 60 leftover
labor hours.
The intermediate step (1.4) solves the equations with basic
variables ![]() and
and ![]() . Here the basic solution is unrealizable. If
you decide to participate only in the basic activities (making deluxe
belts and having leftover labor), you must make 40 belts and have -20
leftover hours (i.e., use 20 more than you have), which you can't do within
your current resources.
. Here the basic solution is unrealizable. If
you decide to participate only in the basic activities (making deluxe
belts and having leftover labor), you must make 40 belts and have -20
leftover hours (i.e., use 20 more than you have), which you can't do within
your current resources.