If 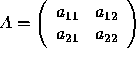 , then det
, then det ![]() .
.
To each square matrix, we associate a number, called its determinant, defined as follows:
If, then det
,
If
, then det
.
For a square matrix A of dimensions ![]() , the determinant
can be obtained as follows. First,
define
, the determinant
can be obtained as follows. First,
define ![]() as the matrix of dimensions
as the matrix of dimensions
![]() obtained from A by deleting row 1 and
column j. Then
obtained from A by deleting row 1 and
column j. Then
det ![]() det
det ![]() det
det ![]() det
det ![]() det
det ![]()
Note that, in this formula, the signs alternate between + and -.
For example, if 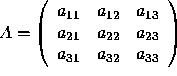 , then
, then
det ![]()
Determinants have several interesting properties. For example, the following statements are equivalent for a square matrix A:
