When we study functions of several variables (see Chapter 3!), we will need the following matrix notions.
A square matrix A is positive definite if ![]() for all nonzero
column vectors x. It is negative definite if
for all nonzero
column vectors x. It is negative definite if ![]() for all
nonzero x. It is positive semidefinite if
for all
nonzero x. It is positive semidefinite if ![]() and negative semidefinite if
and negative semidefinite if ![]() for all x.
These definitions are hard to check directly and you might as well
forget them for all practical purposes.
for all x.
These definitions are hard to check directly and you might as well
forget them for all practical purposes.
More useful in practice are the following properties, which hold when the matrix A is symmetric (that will be the case of interest to us), and which are easier to check.
The ith principal minor of A is the matrix ![]() formed
by the first i rows and columns of A. So, the first
principal minor of A is the matrix
formed
by the first i rows and columns of A. So, the first
principal minor of A is the matrix
![]() , the second
principal minor is the matrix
, the second
principal minor is the matrix
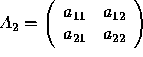 , and so on.
, and so on.
To fix ideas, consider a ![]() symmetic matrix
symmetic matrix
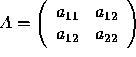 .
.
It is positive definite if:
