Finding global maxima and minima is harder. There is one case that is of interest.
We say that a domain is convex if every line drawn between two points in the domain lies within the domain.
We say that
a function f is convex if the line connecting any two
points lies above the function. That is, for all x,y in the domain
and ![]() , we have
, we have ![]() , as before (see Chapter 2).
, as before (see Chapter 2).
To check that a function is convex on a domain, check that its Hessian matrix H(x) is positive semidefinite for every point x in the domain. To check that a function is concave, check that its Hessian is negative semidefinite for every point in the domain.
![]()
![]()
![]()
![]()
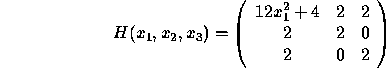
The determinants of the principal minors are det ![]() ,
det
,
det ![]() and det
and det ![]() . So
. So ![]() is positive semidefinite for all
is positive semidefinite for all ![]() in
in ![]() .
This implies that f is convex over
.
This implies that f is convex over ![]() .
.