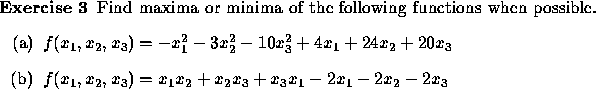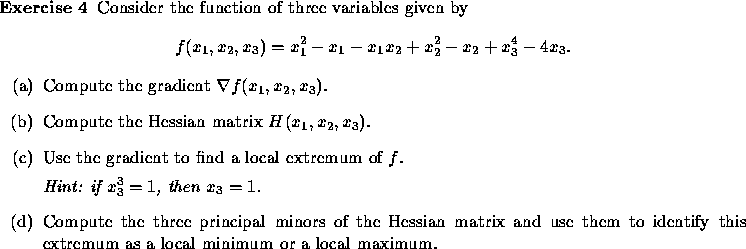Optima can occur in three places:
We will identify the first type of point with Kuhn-Tucker conditions (see next chapter). The second type is found only by ad hoc methods. The third type of point can be found by solving the gradient equations.
In the remainder of this chapter, we discuss the important case
where ![]() .
To identify if a point
.
To identify if a point ![]() with zero gradient is a local maximum or local
minimum, check the Hessian.
with zero gradient is a local maximum or local
minimum, check the Hessian.
![]()
This function is everywhere differentiable, so extrema can only
occur at points ![]() such that
such that ![]() .
.
![]()
This equals 0 iff ![]() or (1,1). The Hessian is
or (1,1). The Hessian is
![]()
So,
![]()
Let ![]() denote the first principal minor of H(0,0) and
let
denote the first principal minor of H(0,0) and
let ![]() denote its second principal minor (see Section 1.6).
Then det
denote its second principal minor (see Section 1.6).
Then det ![]() and det
and det ![]() . Therefore
H(0,0) is neither positive nor negative definite.
. Therefore
H(0,0) is neither positive nor negative definite.
![]()
Its first principal minor has
det ![]() and its second principal minor
has det
and its second principal minor
has det ![]() . Therefore
H(1,1) is positive definite, which implies that
(1,1) is a local minimum.
. Therefore
H(1,1) is positive definite, which implies that
(1,1) is a local minimum.
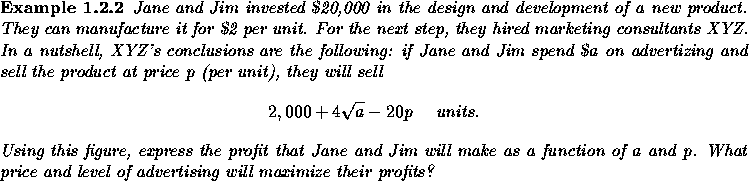
The revenue from sales is ![]() .
.
The production costs are ![]() ,
the development cost is $20,000 and the cost of advertizing is a.
,
the development cost is $20,000 and the cost of advertizing is a.
Therefore, Jane and Jim's profit is
![]()
To find the maximum profit, we compute the partial derivatives of f and set them to 0:
![]()
![]()
Solving this system of two equations yields
![]()
We verify that this is a maximum by computing the Hessian.
![]()
det ![]() and det
and det ![]() at the point p=63.25, a= 15,006.25. So, indeed, this solution
maximizes profit.
at the point p=63.25, a= 15,006.25. So, indeed, this solution
maximizes profit.
![]()
![]()
![]()
Setting these partial derivatives to 0 yields the unique solution
![]() . The Hessian matrix is
. The Hessian matrix is
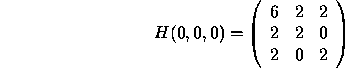
The determinants of the principal minors are det ![]() ,
det
,
det ![]() and det
and det ![]() . So H(0,0,0)
is positive definite and the solution
. So H(0,0,0)
is positive definite and the solution ![]() is a minimum.
is a minimum.