
It is important to know the following differentiation formulas:


For a function f of one variable x, recall that the derivative
f'(x) is equal to the slope of a tangent line at point x.
So, if the function has a positive derivative at point x, then
the function is increasing, and if it has a negative derivative,
it is decreasing.
Since the function and its tangent line are close around point x,
the following formula can be used when ![]() is small.
is small.
![]()
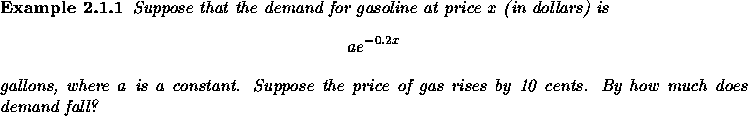
Let ![]() denote the demand for gas at price x.
The rate of change is given by the derivative
denote the demand for gas at price x.
The rate of change is given by the derivative
![]()
Since ![]() , we get
, we get
![]()
So demand drops by 2%. The factor relating change in demand to change in price is known as ``price elasticity of demand'' in economics (You will learn more about this in 45-749 Managerial Economics and in marketing courses such as 45-720 Marketing Management and 45-834 Pricing). Here f'(x) = -0.2 f(x), so price elasticity of demand is -0.2.
