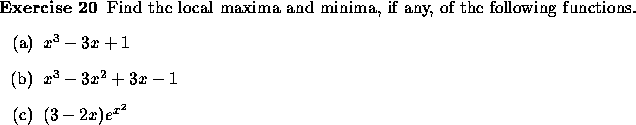Let f be a function of one variable
defined for all x in some domain D. A global
maximum of f is a point 
in D such that 
for all x in D.
For a constant 
,
the neighborhood 
of a point is the set of all
points x such that 
.
A point is a local maximum of f if there exists
such that for all x in
where f(x) is defined.
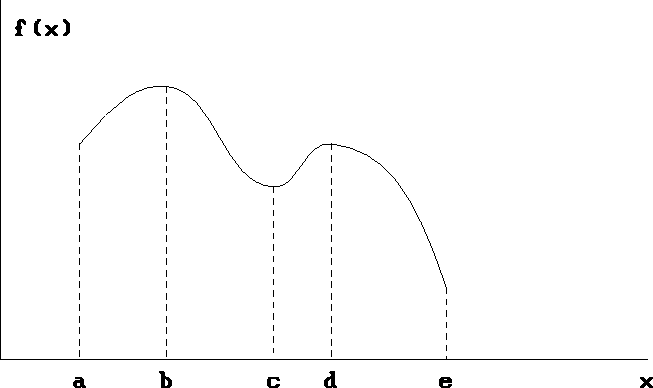
Figure 2.1: local maxima and minima
Similarly one can define local and global minima. In Figure 2.1, the function f is defined for x in domain [ a , e ]. Points b and d are local maxima and b is a global maximum, whereas a, c, and e are local minima and e is a global minimum.
Finding extrema
Extrema, whether they are local or global, can occur in three places:
1. at the boundary of the domain,
2. at a point without a derivative, or
3. at a point with 
.
The last case is particularly important. So we discuss it
further.
Let f be differentiable in a neighborhood of . If
is a local extremum of f, then .
Conversely, if , three possibilities may arise:
is a local maximum, is a local minimum, or neither!!!
To decide between these three possibilities, one may use the
second derivative.
Let f be twice differentiable in a neighborhood of .
and 
then is a local minimum. and 
then is a local maximum. and 
then may or may not be a local
extremum.
Figure 2.2 illustrates these three possibilities.
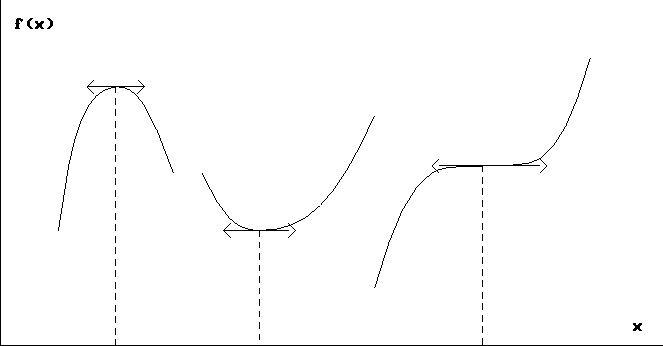
Figure 2.2: , and one of the possibilities
with
The revenue at price x is
We compute the derivative of g and set it to 0.
Since f(x);SPMgt;0 for all x, setting g'(x)=0 implies 1-0.2x=0. So x=5. This is the only possible local optimum. To determine whether it is a maximum or a minimum, we compute the second derivative.
Putting in x=5 shows g''(x);SPMlt;0, so this is a maximum: the oil cartel maximizes its revenue by pricing gasoline at $5 per gallon.
We must first calculate the holding cost (cost of stockpiling). If each order period begins with Q cases and ends with zero cases, and if usage is more or less constant, then the average stock level is Q/2. This means that the average holding cost is hQ/2.
Since each order of Q cases lasts Q/d weeks, the average ordering
cost per week is 
Thus the average total cost per week is
To find Q that minimizes cost, we set to zero the derivative with respect to Q.
This implies that the optimal order quantity is
This is the classical economic order quantity (EOQ) model for inventory management. (You will learn when the EOQ model is appropriate and when to use other inventory models in 45-765).
