Binary Search

Binary search is a very simple idea for solving numerically f(x) = 0.

It requires:

(i)

the function f to be continuous,

(ii)

values (a,b) such that f(a) ;SPMgt; 0 and f(b) ;SPMlt; 0.

Then a desired value such that can be found between the values a and b.

The method consists in computing f(c) for .

• If f(c) ;SPMgt; 0, the procedure is repeated with the values (a,b) replaced by the values (c,b).
• If f(c) ;SPMlt; 0, the procedure is repeated with the values (a,b) replaced by (a,c).
• If f(c) = 0, the procedure terminates as c is the value we are looking for.

This method is easy to program and converges rapidly (20 iterations will give you with 5 significant figures).

The yield r of the bond is given by the equation

Let us denote by f(r) the left-hand-side of this equation. We find r such that f(r) = 0 using binary search.

We start by finding values (a,b) such that f(a) ;SPMgt; 0 and f(b) ;SPMlt; 0. In this case, we expect r to be between 0 and 1. Since f(0) = 500 and f(1) = -743.75, we have our starting values.

Next, we let c = 0.5 (the midpoint) and calculate f(c). Since f(0.5) = -541.975, we replace our range with a=0 and b=0.5 and repeat. When we continue, we get the following table of values:

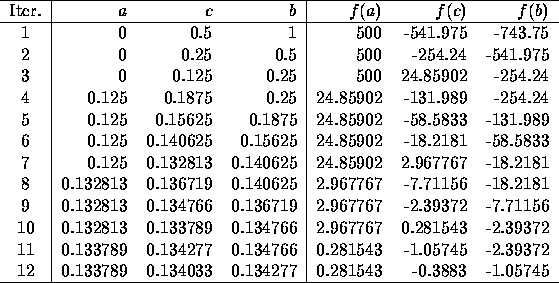
So the yield of the bond is r= 13.4%.

Of course, this routine sort of calculation is perfectly set up for calculation by computer. In particular, we can use Microsoft's Excel (or any spreadsheet program) to do these calculations. On the course home page is a spreadsheet that implements binary search for this problem. We will show this spreadsheet in class. Cells B3:G3 down to B20:G20 contain the body of the table. You can generate the same table by following these steps:

In cell B3, type 0 [comment: this is initial value of a.]

In cell D3, type 1 [comment: this is the initial value of b.]

In cell C3, type =(B3+D3)/2 [comment: this is the middle point c.]

In cell E3, type =100/(1+B3) +100/(1+B3) 2 +100/(1+B3) 3 +1100/(1+B3) 4 -900 [comment: this is f(a).]

Use the Copy Command to copy cell E3 into cells F3 and G3 [comment: cell F3 contains the same function as cell E3, except that B3 is replaced by C3. So cell F3 contains f(c). Similarly, G3 contains f(b).]

In cell B4, type =IF(F3;SPMgt;0,C3,B3) [comment: If F3;SPMgt;0, cell B4 contains C3 and otherwise, cell B4 contains B3.]

In cell D4, type =IF(F3;SPMgt;0,D3,C3)

Use the Copy Command to copy cell B4 down column B

Similarly, copy C3 down column C, D4 down column D, E3 down column E, F3 down column F, and G3 down column G.

Now you should have the full table! Read down column C to find the value of r that makes f(r)=0.

Excel also has an addin called Solver that can search for any particular value for a function. We will also review this system in class (we will use Solver extensively in this course).

Golden Section Search

Golden section search is similar in spirit to binary search. It is used to compute the maximum of a function f(x) defined on an interval [a,b], when the method presented in Section 2.2 is not applicable for one reason or another.

It assumes that

(i)

f is continuous

(ii)

f has a unique local maximum in the interval [a,b].

The golden search method consists in computing f(c) and f(d) for a ;SPMlt; d ;SPMlt; c ;SPMlt; b.

• If f(c) ;SPMgt; f(d), the procedure is repeated with the interval (a,b) replaced by (d,b).
• If f(c) ;SPMlt; f(d), the procedure is repeated with the interval (a,b) replaced by (a,c).

Note: The name ``golden section'' comes from a certain choice of c and d that yields fast convergence, namely c = a + r(b-a) and d = b + r(a-b), where . This is the golden ratio, already known to the ancient greeks.

In this case, we begin with a=0 and b=1. Using golden section search, that gives d=0.382 and c=0.618. The function values are f(a) = 0, f(d) = -0.687, f(c) = -2.493, and f(b) = -7. Since f(c) ;SPMlt; f(d), our new range is a=0, b=.618. Recalculating from the new range gives d=.236, c=.382 (note that our current c was our previous d: it is this reuse of calculated values that gives golden section search its speed). We repeat this process to get the following table:

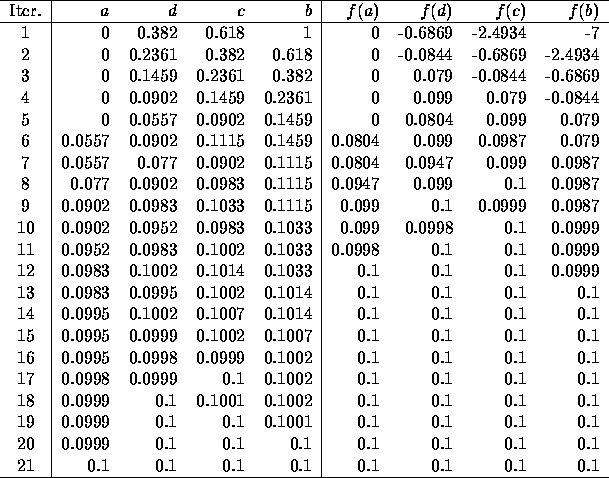
Again we can use Excel to implement golden section search or use Solver to maximize this function directly.