Finding global extrema and checking that we have actually found one
is harder than finding local extrema, in general. There is one nice
case: that of convex and concave functions. A convex function is one
where the line segment connecting two points (x,f(x)) and (y,f(y))
lies above the function. Mathematically,
a function f is convex if, for all x, y and all 
,
See Figure 2.3. The function f is concave if -f is convex.
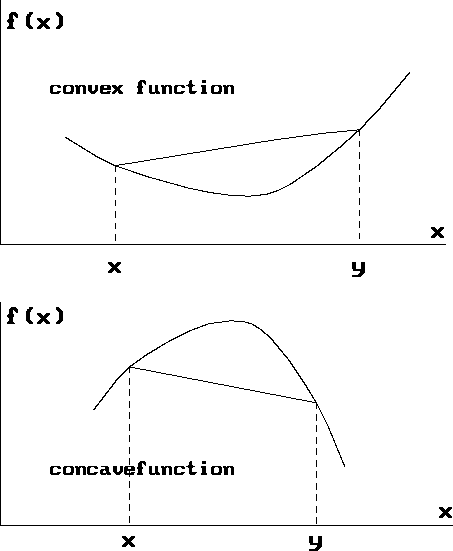
Figure 2.3: Convex function and concave function
There is an easy way to check for convexity when f is twice
differentiable: the function f is convex on some domain [a,b]
if (and only if) 
for all x in the domain.
Similarly, f is concave on some domain [a,b]
if (and only if) 
for all x in the domain.
If f(x) is convex, then any local minimum is also a global minimum.
If f(x) is concave, then any local maximum is also a global maximum.
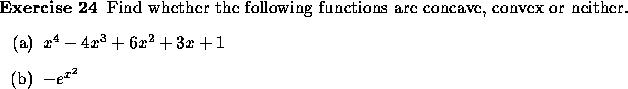
