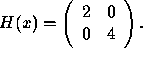Given a
function f of n variables 
,
we define the partial derivative relative to variable 
, written
as 
, to be the derivative of
f with respect to treating all variables except as
constant.
The answer is:
.
Let x denote the vector 
.
With this notation, 
,
, etc.
The gradient of f at x, written 
, is the vector
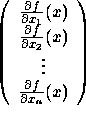. The gradient vector
gives the direction of steepest ascent of the function f
at point x.
The gradient acts like the derivative in that small changes around
a given point 
can be estimated using the gradient.
where 
denotes the vector
of changes.
In this case, 
and 
.
Since 
and 
, we
get
.
So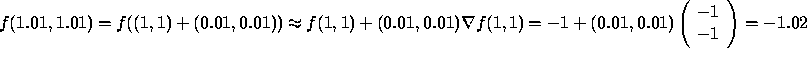 
.
Hessian matrix
Second partials 
are obtained from f(x) by taking
the derivative relative to (this yields the
first partial 
)
and then by taking the derivative of
relative to 
. So we can compute
,
and so on. These values are arranged into the Hessian matrix
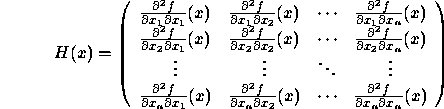
The Hessian matrix is a symmetric matrix, that is
.
Example 3.1.1 (continued):
Find the Hessian matrix of
The answer is
