Suppose we have a problem:
Maximize 
subject to
If we ignore the constraint, we get the solution 
,
which is too large for the constraint. Let us penalize ourselves
for making the constraint too big. We end up with a
function
This function is called the Lagrangian of the problem. The main
idea is to adjust so that we use exactly the right amount of
the resource.
leads to (2,1).
leads to (3/2,0) which uses too little of the
resource.
gives (5/3, 1/3) and the constraint is satisfied
exactly.
We now explore this idea more formally. Given a nonlinear program (P) with equality constraints:
Minimize (or maximize) f(x)
subject to
a solution can be found using the Lagrangian:
(Note: this can also be written 
).
Each 
gives the price associated with constraint
i.
The reason L is of interest is the following:
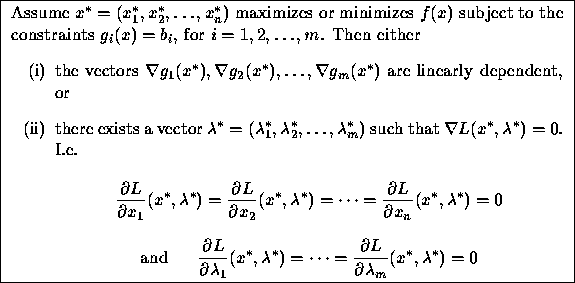
Of course, Case (i) above cannot occur when there is only one constraint. The following example shows how it might occur.
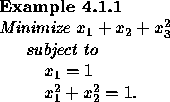
It is easy to check directly that the minimum is acheived
at 
. The associated Lagrangian is
Observe that
and consequently 
does not
vanish at the optimal solution. The reason for this is the following.
Let 
and 
denote
the left hand sides of the constraints. Then 
and 
are linearly dependent vectors.
So Case (i) occurs here!
Nevertheless, Case (i) will not concern us in this course. When solving
optimization problems with equality constraints, we will only look
for solutions 
that satisfy Case (ii).
Note that the equation
is nothing more than
In other words, taking the partials with respect to does
nothing more than return the original constraints.
Once we have found candidate solutions , it is not always
easy to figure out whether they correspond to a minimum, a maximum
or neither. The following situation is one when we can conclude.
If f(x) is concave and all of the
are linear, then any feasible with a corresponding
making 
maximizes f(x)
subject to the constraints.
Similarly, if f(x) is convex and each is linear, then any
with a making minimizes
f(x) subject to the constraints.
Now, the first two equations imply 
. Substituting into the
final equation gives the solution 
, 
and 
, with function value 2/3.
Since 
is convex (its Hessian matrix
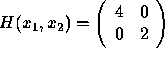is positive definite) and 
is a linear
function, the above solution minimizes subject
to the constraint.
