How do we handle both equality and inequality constraints in (P)? Let (P) be:
Maximize f(x)
Subject to
If you have a program with 
constraints, convert it into 
by
multiplying by -1. Also convert a minimization to a maximization.
The Lagrangian is
The fundamental result is the following:
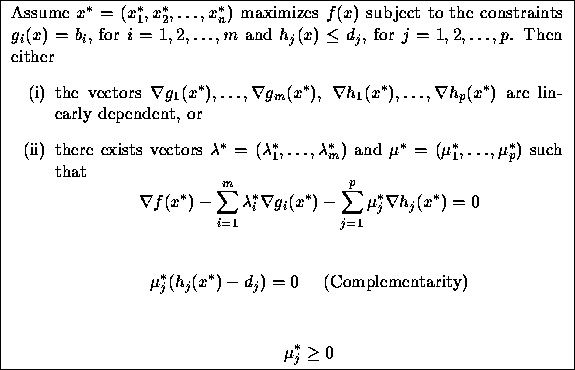
In this course, we will not concern ourselves with Case (i).
We will only look for candidate solutions 
for which we
can find 
and 
satisfying the equations in
Case (ii) above.
In general, to solve these equations, you begin with complementarity and note
that either 
must be zero or 
. Based on the
various possibilities, you come up with one or more candidate
solutions. If there is an optimal solution, then one of your
candidates will be it.
The above conditions are called the Kuhn-Tucker (or Karush-Kuhn-Tucker) conditions. Why do they make sense?
For optimal, some of the inequalities will be tight and some
not. Those not tight can be ignored (and will have corresponding
price 
). Those that are tight can be treated as equalities which
leads to the previous Lagrangian stuff. So
forces either the price to be 0 or the constraint to be
tight.
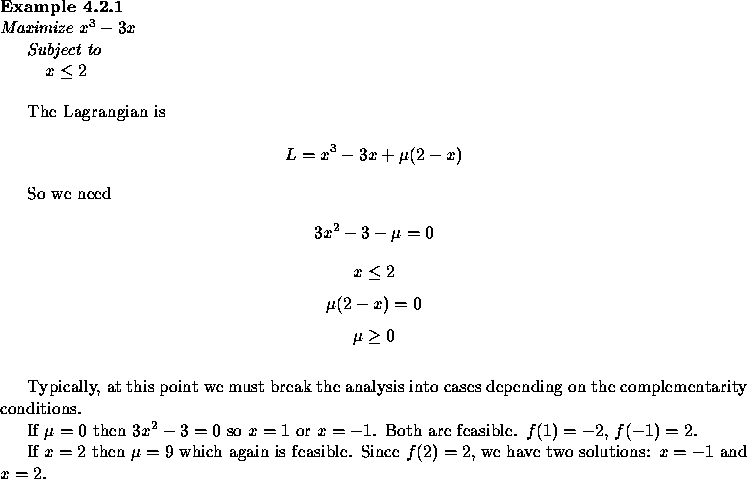
Economic Interpretation
The economic interpretation is essentially the same as the equality
case. If the right hand side of a constraint
is changed by a small amount 
,
then the optimal objective changes by 
,
where is the optimal Lagrange multiplier corresponding
to that constraint. Note that if the
constraint is not tight then the objective does not change (since then
).
Handling Nonnegativity
A special type of constraint is nonnegativity. If you have a
constraint 
, you can write this as 
and use the
above result. This constraint would get a Lagrange multiplier of its own,
and would be treated just like every other constraint.
An alternative is to treat nonnegativity implicitly. If 
must be
nonnegative:
for x to be feasible.
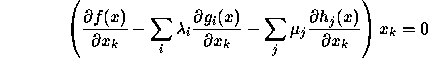
Sufficiency of conditions
The Karush-Kuhn-Tucker conditions give us candidate
optimal solutions . When are these conditions sufficient
for optimality? That is, given with and
satisfying the KKT conditions, when can we be certain that it is an
optimal solution?
The most general condition available is:
While it is straightforward to determine if the objective is concave by computing its Hessian matrix, it is not so easy to tell if the feasible region is convex. A useful condition is as follows:
The feasible region is convex if all of the 
are linear and
all of the 
are convex.
If this condition is satisfied, then any point that satisfies the KKT conditions gives a point that maximizes f(x) subject to the constraints.
Review of Optimality Conditions.
The following reviews what we have learned so far:
Single Variable (Unconstrained)
Solve f'(x) = 0 to get candidate .
If 
then is a local min.
then is a local max.
If f(x) is convex then a local min is a global min.
f(x) is concave then a local max is a global max.
Multiple Variable (Unconstrained)
Solve 
to get candidate .
If 
is positive definite then is a local min.
is negative definite is a local max.
If f(x) is convex then a local min is a global min.
f(x) is concave then a local max is a global max.
Multiple Variable (Equality constrained)
Form Lagrangian 
Solve 
to get candidate (and
).
Best is optimum if optimum exists.
Multiple Variable (Equality and Inequality constrained)
Put into standard form (maximize and constraints)
Form Lagrangian 
Solve
to get candidates (and , ).
Best is optimum if optimum exists.
Any is optimum if f(x) concave, convex,
linear.