The first change we will consider is changing a cost value by
in the original problem. We are given the original problem
and an optimal tableau. If we had
done exactly the same calculations beginning with the modified
problem, we would have had the same final tableau except that the
corresponding cost entry would be lower (this is because we
never do anything except add or subtract scalar multiples of
Rows 1 through m to other rows; we never add or subtract Row 0
to other rows). For example, take the problem
Max 3x+2y Subject to x+y <= 4 2x+y <= 6 x,y >= 0
The optimal tableau to this problem (after adding 
and 
as
slacks to place in standard form) is:
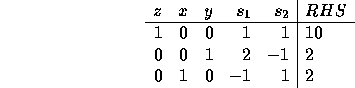
Suppose the cost for x is changed to 
in the original formulation,
from its previous value 3.
After doing the same operations as before, that is the same pivots,
we would end up with the tableau:
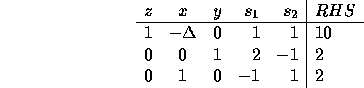
Now this is not the optimal tableau: it does not have a correct
basis (look at the column of x).
But we can make it correct in form while keeping the same
basic variables by adding times the last row to the cost row.
This gives the tableau:
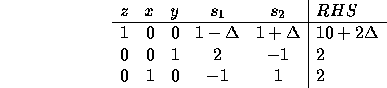
Note that this tableau has the same basic variables and the same variable values (except for z) that our previous solution had. Does this represent an optimal solution? It does only if the cost row is all non-negative. This is true only if
which holds for 
. For any
in that range, our previous basis (and variable values) is
optimal. The objective changes to 
.
In the previous example, we changed the cost of a basic variable. Let's go through another example. This example will show what happens when the cost of a nonbasic variable changes.
Max 3x+2y + 2.5w Subject to x+y +2w <= 4 2x+y +2w <= 6 x,y,w >= 0
Here, the optimal tableau is :
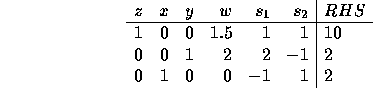
Now suppose we change the cost on w from 2.5 to 
in the formulation. Doing the same
calculations as before will result in the tableau:
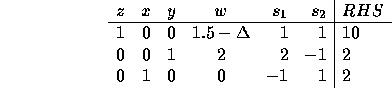
In this case, we already have a valid tableau. This will represent an
optimal solution if 
, so 
. As long
as the objective coefficient of w is no more than 2.5+1.5=4 in the
original formulation, our solution of x=2,y=2 will remain optimal.
The value in the cost row in the simplex tableau is called the reduced cost. It is zero for a basic variable and, in an optimal tableau, it is non-negative for all other variables (for a maximization problem).
Summary: Changing objective function values in the original formulation will result in a changed cost row in the final tableau. It might be necessary to add a multiple of a row to the cost row to keep the form of the basis. The resulting analysis depends only on keeping the cost row non-negative.