For these types of changes, we concentrate on maximization
problems with all ![]() constraints. Other cases are handled
similarly.
constraints. Other cases are handled
similarly.
Take the following problem:
The optimal tableau, after adding slacks ![]() and
and ![]() is
is
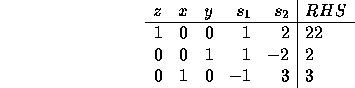
Now suppose instead of 12 units in the first constraint, we only had
11. This is equivalent to forcing ![]() to take on value 1.
Writing the constraints in the optimal tableau
long-hand, we get
to take on value 1.
Writing the constraints in the optimal tableau
long-hand, we get
![]()
![]()
![]()
If we force ![]() to 1 and keep
to 1 and keep ![]() at zero (as a nonbasic variable
should be), the new solution would be z = 21, y=1, x=4. Since
all variables are nonnegative, this is the optimal solution.
at zero (as a nonbasic variable
should be), the new solution would be z = 21, y=1, x=4. Since
all variables are nonnegative, this is the optimal solution.
In general, changing the amount of the right-hand-side from 12 to
![]() in the first constraint changes the tableau to:
in the first constraint changes the tableau to:
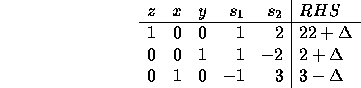
This represents an optimal tableau as long as the righthand side is
all non-negative. In other words, we need ![]() between -2 and
3 in order for the basis not to change. For any
between -2 and
3 in order for the basis not to change. For any ![]() in that
range, the optimal objective will be
in that
range, the optimal objective will be ![]() . For example, with
. For example, with
![]() equals 2, the new objective is 24 with y=4 and x=1.
equals 2, the new objective is 24 with y=4 and x=1.
Similarly, if we change the right-hand-side of the second constraint
from 5 to ![]() in the original formulation, we get an
objective of
in the original formulation, we get an
objective of ![]() in the final tableau, as long
as
in the final tableau, as long
as ![]() .
.
Perhaps the most important concept in sensitivity analysis is the
shadow price ![]() of a constraint:
If the RHS of Constraint i changes by
of a constraint:
If the RHS of Constraint i changes by ![]() in the original
formulation, the optimal objective value changes by
in the original
formulation, the optimal objective value changes by ![]() .
The shadow price
.
The shadow price ![]() can be found in the optimal tableau.
It is the reduced cost of the slack
variable
can be found in the optimal tableau.
It is the reduced cost of the slack
variable ![]() . So it is found in the cost row (Row 0)
in the column corresponding the slack for Constraint i.
In this case,
. So it is found in the cost row (Row 0)
in the column corresponding the slack for Constraint i.
In this case, ![]() (found in Row 0 in the column of
(found in Row 0 in the column of ![]() )
and
)
and ![]() (found in Row 0 in the column of
(found in Row 0 in the column of ![]() ).
The value
).
The value ![]() is really the marginal value of the
resource associated with Constraint i. For example, the
optimal objective value (currently 22)
would increase by 2 if we could increase the RHS of
the second constraint by
is really the marginal value of the
resource associated with Constraint i. For example, the
optimal objective value (currently 22)
would increase by 2 if we could increase the RHS of
the second constraint by ![]() . In other words, the marginal
value of that resource is 2, i.e. we are willing to pay up to
2 to increase the right hand side of the second constraint by 1 unit.
You may have noticed the similarity of interpretation between shadow
prices in linear programming and Lagrange multipliers in constrained
optimization. Is this just a coincidence? Of course not. This parallel
should not be too surprising since, after all, linear programming
is a special case of constrained optimization. To derive this
equivalence (between shadow prices and optimal Lagrange multipiers),
one could write the KKT conditions for the linear
program...but we will skip this in this course!
. In other words, the marginal
value of that resource is 2, i.e. we are willing to pay up to
2 to increase the right hand side of the second constraint by 1 unit.
You may have noticed the similarity of interpretation between shadow
prices in linear programming and Lagrange multipliers in constrained
optimization. Is this just a coincidence? Of course not. This parallel
should not be too surprising since, after all, linear programming
is a special case of constrained optimization. To derive this
equivalence (between shadow prices and optimal Lagrange multipiers),
one could write the KKT conditions for the linear
program...but we will skip this in this course!
In summary, changing the right-hand-side of a constraint is identical to setting the corresponding slack variable to some value. This gives us the shadow price (which equals the reduced cost for the corresponding slack) and the ranges.