This game has two pure strategy equilibria, namely one of the two
firms enters the
market niche and the other stays out. But, unlike the games we have
encountered thus far, neither player has a dominant strategy.
When a player has no dominant strategy, she should consider playing a
mixed strategy. In a mixed strategy, each of the various
pure strategies is played with some probability, say 
for
Strategy 1, 
for Strategy 2, etc with 
.
What would be the best mixed strategies for Firms A and B? Denote by
the probability that Firm A enters the market niche. Therefore 
is
the probability that Firm A stays out. Similarly, Firm B enters the
niche with probability 
and stays out with probability 
.
The key insight to a mixed strategy
equilibrium is the following. Every pure strategy that is played
as part of a mixed strategy equilibrium has the same expected value.
If one pure strategy is expected to pay less than another, then it
should not be played at all. The pure strategies that are not
excluded should be expected to pay the same. We now apply this principle.
The expected value of the ``Enter'' strategy for Firm A, when
Firm B plays its mixed strategy, is
The expected value of the ``Stay out'' strategy for Firm A is
.
Setting 
we get
Using 
, we obtain
Similarly,
As you can see, the payoffs of this mixed strategy equilibrium,
namely (0,0), are inefficient. One of these firms could make
a lot of money by entering the market niche, if it was sure that
the other would not enter the same niche. This assurance
is precisely what is missing. Each firm has exactly the
same right to enter the market niche. The only way for both
firms to exercise this right is to
play the inefficient, but symmetrical, mixed strategy equilibrium.
In many industrial markets, there is only room for a few firms -
a situation known as natural oligopoly. Chance plays a major
role in the identity of the firms that ultimately enter such
markets. If too many firms enter, there are losses all around and eventually
some firms must exit. From the mixed strategy equilibrium, we can actually
predict how often two firms enter a market niche when there is only room
for one: with the above data, the probability of entry by either firm is
2/3, so the probability that both firms enter is 
. That is
a little over 44% of the time! This is the source
of the inefficiency. The efficient solution has total payoff
of 100, but is not symmetrical. The fair solution pays each player the same
but is inefficient. These two principles, efficiency and fairness, cannot
be reconciled in a game like Market Niche.
Once firms recognize this, they can try to find mecanisms to reach
the efficient solution. For example, they may consider side
payments. Or firms might simply attempt to scare off competitors
by announcing their intention of moving into the market niche before
they actually do so.
An important case where mixed strategies at equilibrium are always efficient is the case of constant-sum games. Interestingly, the optimal mixed strategies can be computed using linear programming, one linear program for each of the two players. We illustrate these ideas on an example.
The payoff matrix is as follows.
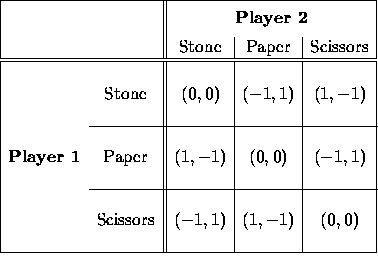
Suppose Player 1 chooses the mixed strategy 
, where
The expected payoff of Player 1 is 
when Player 2 plays Stone,
when Player 2 plays Paper and 
when Player 2 plays Scissors.
The best Player 2 can do is to achieve the minimum of these three
values, namely 
. Player 1, on the other
hand, should try to make the quantity v as large as possible.
So, Player 1 should use probabilities 
, 
and 
that
maximize . This can be
written as the following linear program.
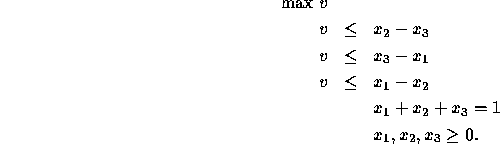
Similarly, we obtain Player 2's optimal mixed strategy 
, where
by solving the linear program
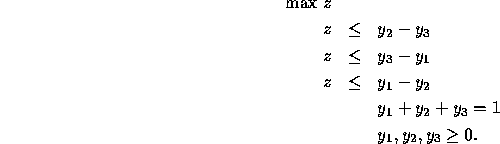
For the Stone, Paper, Scissors game, the optimal solutions are
and 
with 
.
In general, for any
2-person zero-sum game, let 
and 
be the optima
of the linear programs for Players 1 and 2 respectively.
Because of the special form of these linear programs,
it can be shown that 
.
So, the payoff at equilibrium is 
.
The fact that, for each player, the equilibrium solutions
are the optimal solutions of a linear has another
consequence: All equilibrium
solutions have the same payoff.