next up previous contents
Next: Applications Up: Data Envelopment Analysis Previous: Graphical Example

Using Linear Programming

Data Envelopment Analysis, is a linear programming procedure for a frontier analysis of inputs and outputs. DEA assigns a score of 1 to a unit only when comparisons with other relevant units do not provide evidence of inefficiency in the use of any input or output. DEA assigns an efficiency score less than one to (relatively) inefficient units. A score less than one means that a linear combination of other units from the sample could produce the same vector of outputs using a smaller vector of inputs. The score reflects the radial distance from the estimated production frontier to the DMU under consideration.

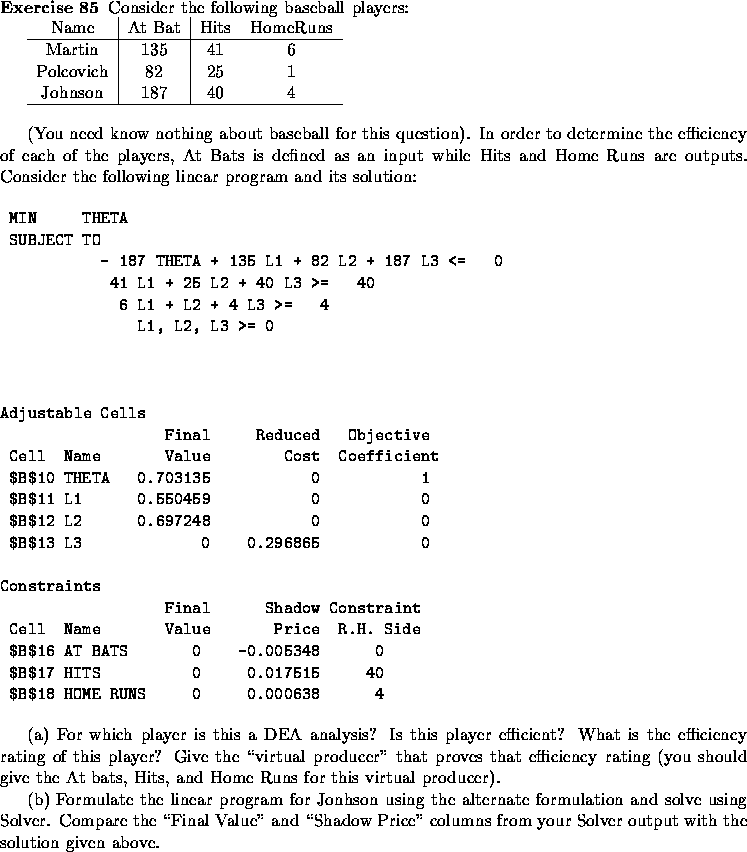
There are a number of equivalent formulations for DEA. The most direct formulation of the exposition I gave above is as follows:

Let tex2html_wrap_inline9316 be the vector of inputs into DMU i. Let tex2html_wrap_inline9320 be the corresponding vector of outputs. Let tex2html_wrap_inline9322 be the inputs into a DMU for which we want to determine its efficiency and tex2html_wrap_inline9324 be the outputs. So the X's and the Y's are the data. The measure of efficiency for tex2html_wrap_inline9330 is given by the following linear program:

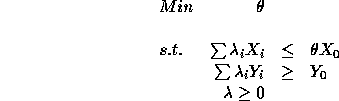
displaymath9308

where tex2html_wrap_inline6982 is the weight given to DMU i in its efforts to dominate DMU 0 and tex2html_wrap_inline9336 is the efficiency of DMU 0. So the tex2html_wrap_inline6950 's and tex2html_wrap_inline9336 are the variables. Since DMU 0 appears on the left hand side of the equations as well, the optimal tex2html_wrap_inline9336 cannot possibly be more than 1. When we solve this linear program, we get a number of things:

  1. The efficiency of DMU 0 ( tex2html_wrap_inline9336 ), with tex2html_wrap_inline9346 meaning that the unit is efficient.
  2. The unit's ``comparables'' (those DMU with nonzero tex2html_wrap_inline6950 ).
  3. The ``goal'' inputs (the difference between tex2html_wrap_inline9322 and tex2html_wrap_inline9352 )
  4. Alternatively, we can keep inputs fixed and get goal outputs ( tex2html_wrap_inline9354 )

DEA assumes that the inputs and outputs have been correctly identified. Usually, as the number of inputs and outputs increase, more DMUs tend to get an efficiency rating of 1 as they become too specialized to be evaluated with respect to other units. On the other hand, if there are too few inputs and outputs, more DMUs tend to be comparable. In any study, it is important to focus on correctly specifying inputs and outputs.

example4047

The linear programs for evaluating the 3 DMUs are given by:

The solution to each of these is as follows:

Note that DMUs 1 and 3 are overall efficient and DMU 2 is inefficient with an efficiency rating of 0.773333.

Hence the efficient levels of inputs and outputs for DMU 2 are given by:

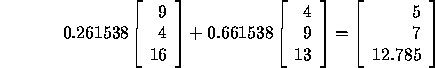
Note that the outputs are at least as much as the outputs currently produced by DMU 2 and inputs are at most as big as the 0.773333 times the inputs of DMU 2. This can be used in two different ways: The inefficient DMU should target to cut down inputs to equal at most the efficient levels. Alternatively, an equivalent statement can be made by finding a set of efficient levels of inputs and outputs by dividing the levels obtained by the efficiency of DMU 2. This focus can then be used to set targets primarily for outputs rather than reduction of inputs.

Alternate Formulation

There is another, probably more common formulation, that provides the same information. We can think of DEA as providing a price on each of the inputs and a value for each of the outputs. The efficiency of a DMU is simply the ratio of the inputs to the outputs, and is constrained to be no more than 1. The prices and values have nothing to do with real prices and values: they are an artificial construct. The goal is to find a set of prices and values that puts the target DMU in the best possible light. The goal, then is to

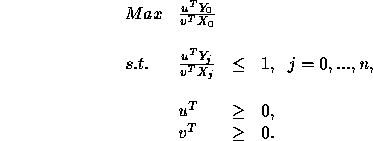
displaymath9309

Here, the variables are the u's and the v's. They are vectors of prices and values respectively.

This fractional program can be equivalently stated as the following linear programming problem (where Y and X are matrices with columns tex2html_wrap_inline9368 and tex2html_wrap_inline9370 respectively).

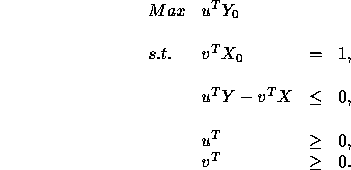
displaymath9310

We denote this linear program by (D). Let us compare it with the one introduced earlier, which we denote by (P):

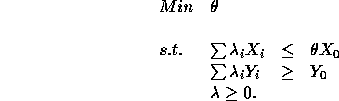
displaymath9311

To fix ideas, let us write out explicitely these two formulations for DMU 2, say, in our example.

Formulation (P) for DMU 2: 

min                     THETA
st
-5 L1 - 8 L2 - 7 L3 + 8 THETA >= 0
-14L1 -15 L2 -12 L3 + 15THETA >= 0
 9 L1 + 5 L2 + 4 L3           >= 5
 4 L1 + 7 L2 + 9 L3           >= 7
 16L1 +10 L2 +13 L3           >= 10
L1>=0, L2>=0, L3>=0

Formulation (D) for DMU 2: 

max             5 U1 + 7 U2 + 10 U3 
st
- 5 V1 - 14V2 + 9 U1 + 4 U2 + 16 U3 <= 0
- 8 V1 - 15V2 + 5 U1 + 7 U2 + 12 U3 <= 0
- 7 V1 - 12V2 + 4 U1 + 9 U2 + 13 U3 <= 0
  8 V1 + 15V2                        = 1
    V1>=0, V2>=0, U1>=0, U2>=0,  U3>=0

Formulations (P) and (D) are dual linear programs! These two formulations actually give the same information. You can read the solution to one from the shadow prices of the other. We will not discuss linear programming duality in this course. You can learn about it in some of the OR electives.

exercise4106

next up previous contents
Next: Applications Up: Data Envelopment Analysis Previous: Graphical Example

Michael A. Trick
Mon Aug 24 16:30:59 EDT 1998