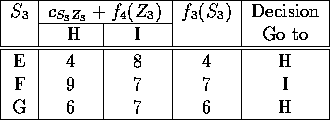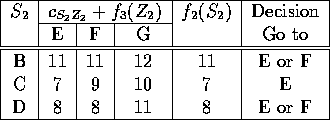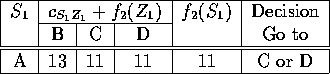A second example

Dynamic programming may look somewhat familiar. Both our shortest path algorithm and our method for CPM project scheduling have a lot in common with it.

Let's look at a particular type of shortest path problem. Suppose we wish to get from A to J in the road network of Figure 2.

  
Figure 2: Road Network

The numbers on the arcs represent distances. Due to the special structure of this problem, we can break it up into stages. Stage 1 contains node A, stage 2 contains nodes B, C, and D, stage 3 contains node E, F, and G, stage 4 contains H and I, and stage 5 contains J. The states in each stage correspond just to the node names. So stage 3 contains states E, F, and G.

If we let S denote a node in stage j and let be the shortest distance from node S to the destination J, we can write

where denotes the length of arc SZ. This gives the recursion needed to solve this problem. We begin by setting . Here are the rest of the calculations:

Stage 4.

During stage 4, there are no real decisions to make: you simply go to your destination J. So you get:

• by going to J,
• by going to J.

Stage 3.

Here there are more choices. Here's how to calculate . From F you can either go to H or I. The immediate cost of going to H is 6. The following cost is . The total is 9. The immediate cost of going to I is 3. The following cost is for a total of 7. Therefore, if you are ever at F, the best thing to do is to go to I. The total cost is 7, so .

The next table gives all the calculations:

You now continue working back through the stages one by one, each time completely computing a stage before continuing to the preceding one. The results are:

Stage 2.

Stage 1.