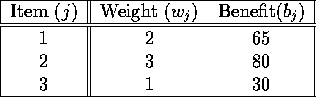
Table 4: Knapsack Items
The knapsack problem is a particular type of integer program with just one constraint. Each item that can go into the knapsack has a size and a benefit. The knapsack has a certain capacity. What should go into the knapsack so as to maximize the total benefit? As an example, suppose we have three items as shown in Table 4, and suppose the capacity of the knapsack is 5.
The stages represent the items: we have three stages j=1,2,3.
The state ![]() at stage j represents the total weight of
items j and all following items in the knapsack.
The decision at stage j is how many items j to place in the
knapsack. Call this value
at stage j represents the total weight of
items j and all following items in the knapsack.
The decision at stage j is how many items j to place in the
knapsack. Call this value ![]() .
.
This leads to the following recursive formulas: Let ![]() be the
value of using
be the
value of using ![]() units of capacity for items j and following.
Let
units of capacity for items j and following.
Let ![]() represent the largest integer less than or
equal to a.
represent the largest integer less than or
equal to a.