Not every recursion must be additive. Here is one example where we multiply to get the recursion.
A student is currently taking three courses. It is important that he
not fail all of them. If the probability of failing French is 
,
the probability of failing English is 
, and the probability of
failing Statistics is 
, then the probability of failing all of
them is 
. He has left himself with four hours to study.
How should he minimize his probability of failing all his courses?
The following gives the probability of failing each course given he
studies for a certain number of hours on that subject, as shown in
Table 6.
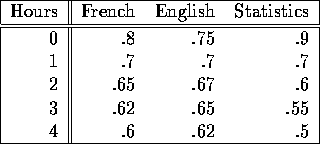
Table 6: Student failure probabilities.
(What kind of student is this?) We let stage 1 correspond to studying
French, stage 2 for English, and stage 3 for Statistics. The state
will correspond to the number of hours studying for that stage and all
following stages. Let 
be the probability of failing t and
all following courses, assuming x hours are available. Denote the
entries in the above table as 
, the probability of failing
course t given k hours are spent on it.
The final stage is easy:
The recursion is as follows:
We can now solve this recursion:
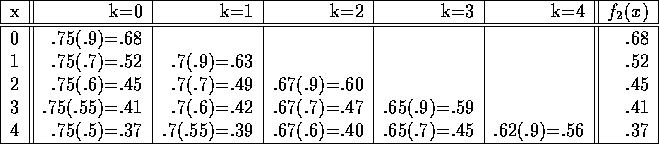
So, the optimum way of dividing time between studying English and Statistics is to spend it all on Statistics.
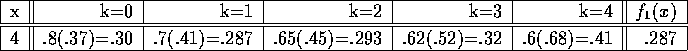
The overall optimal strategy is to spend one hour on French, and three on Statistics. The probability of failing all three courses is about 29%.