Data Envelopment Analysis, is a linear programming procedure for a frontier analysis of inputs and outputs. DEA assigns a score of 1 to a unit only when comparisons with other relevant units do not provide evidence of inefficiency in the use of any input or output. DEA assigns an efficiency score less than one to (relatively) inefficient units. A score less than one means that a linear combination of other units from the sample could produce the same vector of outputs using a smaller vector of inputs. The score reflects the radial distance from the estimated production frontier to the DMU under consideration.
There are a number of equivalent formulations for DEA. The most direct formulation of the exposition I gave above is as follows:
Let 
be the vector of inputs into DMU i. Let 
be the
corresponding vector of outputs. Let 
be the inputs into a DMU
for which we want to determine its efficiency and 
be the
outputs.
We would like to find the best combination of DMUs that dominates DMU 0. This problem can be written as:
The measure of efficiency for 
is given by the following
fractional program:
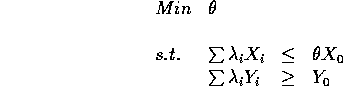
where 
is the weight given to DMU i in its efforts to
dominate DMU 0 and 
is the efficiency of DMU 0. In general, we
should include DMU 0 on the left hand side of the equations. Then,
the optimal cannot possibly be more than 1. When we solve
this linear program, we get a number of things:
), with 
meaning that
the unit is efficient.
). and 
)
)
There is another, probably more common formulation, that provides the same information. We can think of DEA as providing a price on each of the inputs and a value for each of the outputs. The efficiency of a DMU is simply the ration of the inputs to the outputs, and is constrained to be no more than 1. The prices and values have nothing to do with real prices and values: they are an artificial construct. The goal is to find a set of prices and values that puts the target DMU in the best possible light. The goal, then is to
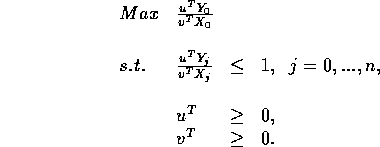
Here u and v are vectors of prices and values respectively.
Sometimes, people require u and v to be strictly positive, by
forcing them to be 
for a very small epsilon. This
change makes very little difference:
the dual variables associated with
these constraints have a nice interpretation and it makes certain
advanced analysis a bit easier..
This linear fractional program can be equivalently stated
as the following linear programming problem
(where Y and X are matrices with columns 
and 
respectively).
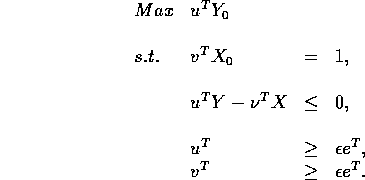
These two formulations actually give the same information. You can read the solution to one from the shadow prices of the other.
DEA assumes that the inputs and outputs have been correctly identified. Usually, as the number of inputs and outputs increase, more DMUs tend to get an efficiency rating of 1 as they become too specialized to be evaluated with respect to other units. On the other hand, if there are too few inputs and outputs, more DMUs tend to be comparable. In any study, it is important to focus on correctly specifying inputs and outputs.