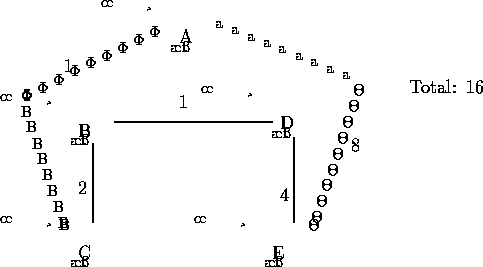
Figure 2: Heuristic Solution
A second solution technique, and probably the most used heuristic technique, is the greedy technique. The general idea is as follows: begin with no assignments of values to variables. At each step, assign one variable a value. The choice of variable and value are that which minimizes the increase in the objective function (for minimization). This is a general approach, not an algorithm. Let's see how to implement it for the TSP. There are a number of different possibilities.
One natural heuristic is to start at any node. From there, go to the closest (cheapest) unvisited node. Continue along until you have visited all the nodes, at which point you return to the start. On our example, we get the solution in figure 2.
This heuristic is called nearest neighbor, for obvious reasons. In our example, nearest neighbor gives a solution of length 16. Is this optimal? We could try other heuristics and see if we could find a better solution. Later we will see methods, called relaxations, that give a lower bound on the solution value.
There are many other greedy algorithms for the TSP. For instance, there is also the possibility of adding edges throughout the graph, always making certain we can complete the tour. In our example, we would first add the edge AC, then BD, then AD, then BE, then CE, for a tour with cost 18.
Greedy heuristics are distinguished by the property that once a decision is made, it is never changed. Once an edge is added to the solution, it is never taken out. Greedy heuristics generally do much better than random. Unfortunately, in many cases there is very little opportunity for randomization, so we are stuck with just one (or just a few) solutions.