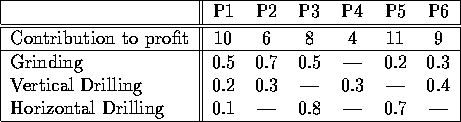
Table 1: Production Data
Due October 10, 1996. You may work in groups of up to four people.
A factory makes six products (P1 to P6) on the following machines: four grinders, two vertical drills, and three horizontal drills. Each product yields a certain contribution to profit (defined as selling price minus cost of raw materials and other variable costs). These profits (in $/unit), together with the unit production times (in hours) are given in Table 1. A dash indicates that a product does not require a process.
In the coming six months (beginning in August), certain machines will be down for maintenance (for the entire month). These machines will be as follows:

The orders for each product in each month are given in Table 2. Unmet demand in any given month results in lost sales. It is possible to hold inventories of each product at at cost of $0.50 per unit per month. There are no inventories at present, and no inventories desired at the end of January.
The factory works a six day week with two 8-hour shifts per day. Assume that there are 24 working days in every month.
A previous consultant created a linear program to optimize production without considering machine downtime due to maintenance. This spreadsheet is available at the web site http://mat.gsia.cmu.edu/mstc/. Your task is to update this model so as to consider machine downtime and answer the following questions:
After solving both of these, compare the models and corresponding solutions. Some aspects to consider are problem size, computation time, number of branches enumerated, initial linear programming solution quality, and any other aspects you deem important.
Determine constraints for each of your two integer programming formulations, and solve. How do the two formulations compare for this problem? Consider ease of formulation, computation time, and any other relevant aspects.
Note: In all the questions, you can terminate a computer run if SOLVER requires more than ten minutes to solve the problem. Report all the information you can gather on such partial runs.