Solutions to Some Optional Problems

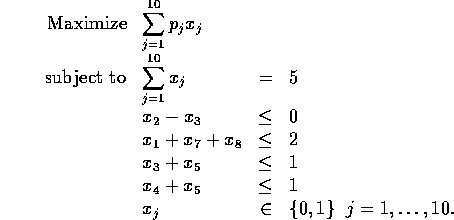
Exercise 1: The formulation is:

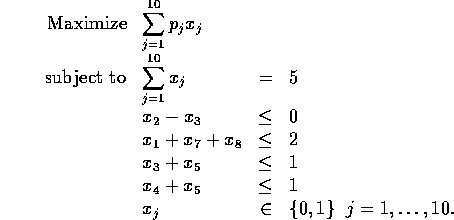
Exercise 2: Let be a 0,1 variable which equals 1 if route j is used, 0 otherwise. Then the vehicle routing problem can be formulated as a set covering problem:

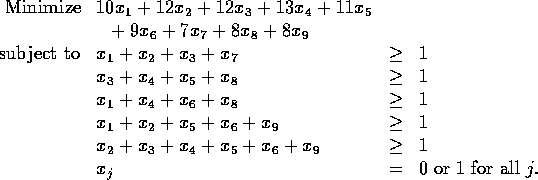
Exercise 3: Let starting time of operation j.

Then the formulation is:

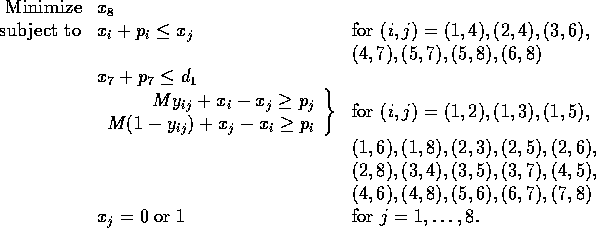
The first set of constraints are the precedence constraints and the last two sets are the noninterference constraints.

Exercise 4: First we solve the problem as a linear program with LINDO. The solution is , . Rounding it yields , which fails to satisfy the constraint .

In fact, the only feasible integer solution is

and it cannot be obtained by simple rounding.

Exercise 5: The enumeration tree is given in Figure 8.

  
Figure 8: Enumeration tree

Three optimum integer solutions were found, namely

each with value z=5.

Exercise 6

From the enumeration tree of Exercise 5, we see that only one branching is necessary since both subproblems and are inactive by reason of integrality. The better solution is with value .

Exercise 7

MAX 4 X1 + 7 X2 + 6 X3 + 5 X4 + 4 X5
SUBJECT TO
   2) 5 X1 + 8 X2 + 3 X3 + 2 X4 + 7 X5 <= 112
   3) X1 + 8 X2 + 6 X3 + 5 X4 + 4 X5 <= 109
END
GIN 5

ENUMERATION COMPLETE. BRANCHES= 6 PIVOTS= 20

OBJECTIVE FUNCTION VALUE  151.000

VARIABLE      VALUE      REDUCED COST
      X1      14.000           -4.000
      X2        .000           -7.000
      X3        .000           -6.000
      X4      19.000           -5.000
      X5        .000           -4.000

Exercise 8

Since does not satisfy the knapsack constraint , it follows that must hold for all solutions of the knapsack problem.

Similarly for .

MAX 8 X1 + 11 X2 + 6 X3 + 4 X4 
SUBJECT TO
   2) 5 X1 + 7 X2 + 4 X3 + 3 X4  <= 14
   3) X1 +  X2 +  X3 <= 2
   3) X1 +  X2 +  X4 <= 2
END
SUB X1 1
SUB X2 1
SUB X3 1
SUB X4 1

OBJECTIVE FUNCTION VALUE  21.000

VARIABLE      VALUE      REDUCED COST
      X1        .000            0.000
      X2       1.000           -3.000
      X3       1.000           -2.000
      X4       1.000            0.000