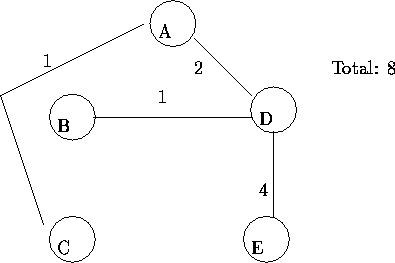
Figure 1: MST relaxation
Assuming that all of the costs are nonnegative, the optimal tour must be at least as long as that for the minimum spanning tree. The reason for this is that removing any edge from a tour forms a spanning tree. The minimum spanning tree must be even cheaper that that. Therefore the minimum spanning tree is cheaper than the cheapest tour.
The minimum spanning tree for our example is in figure 1.
This means that the optimal tour is somewhere between 16 (the heuristic solution we have) and 8 (the relaxation value) inclusive. Although it may not be much to say we are within 8 of optimal with nearest neighbor, it is some information.