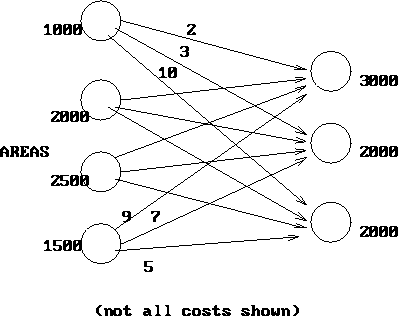
Figure 3: Snow Transportation Network
Consider the following snow removal problem: there are a number of districts in a city. After a snowfall, the snow in each area must be moved out of the district into a convenient location. In Montreal (from where I am taking this example), these locations are large grates (leading to the sewer system), a couple large pits, and a couple entry points to the river. Each of these destinations has a capacity. The goal is to minimize the distance traveled to handle all of the snow.
This problem is an example of a transportation problem. In such a problem, there are a set of nodes called sources, and a set of nodes called destinations. All arcs go from a source to a destination. There is a per-unit cost on each arc. Each source has a supply of material, and each destination has a demand. We assume that the total supply equals the total demand (possibly adding a fake source or destination as needed). For the snow removal problem, the network might look like that in figure 3.

Figure 3: Snow Transportation Network
Transportation problems are often used in, surprise, transportation planning. For instance, in an application where goods are at a warehouse, one problem might be to assign customers to a warehouse so as to meet their demands. In such a case, the warehouses are the sources, the customers are the destinations, and the costs represent the per-unit transportation costs.