Exercise 1: The formulation is:
Exercise 2: Let 
be a 0,1 variable which equals 1 if route
j is used, 0 otherwise. Then the vehicle routing problem can be formulated
as a set covering problem:
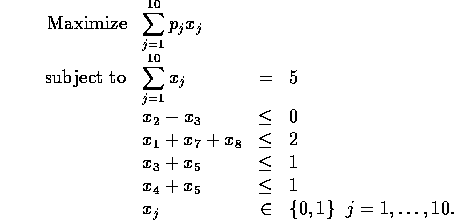
Exercise 3: Let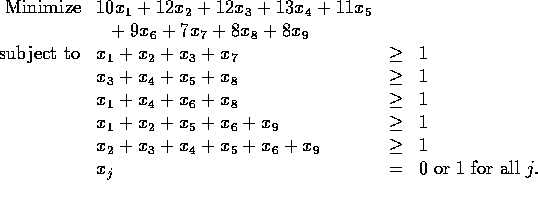 
starting time of operation j.
Then the formulation is:
The first set of constraints are the precedence constraints and the last two sets are the noninterference constraints.
Exercise 4: First we solve the problem as a linear program with LINDO.
The solution is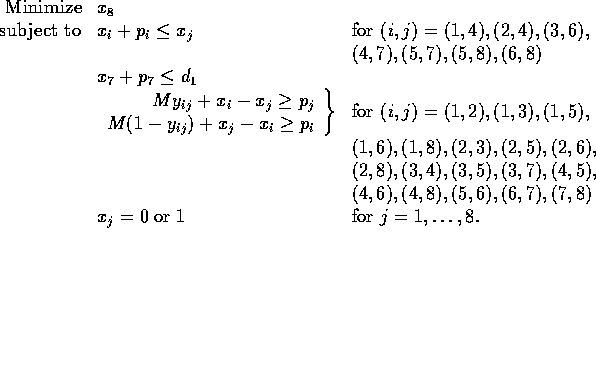 
, 
. Rounding it yields 
,
which fails to satisfy the constraint 
.
In fact, the only feasible integer solution is
and it cannot be obtained by simple rounding.
Exercise 5: The enumeration tree is given in Figure 9.
Three optimum integer solutions were found, namely
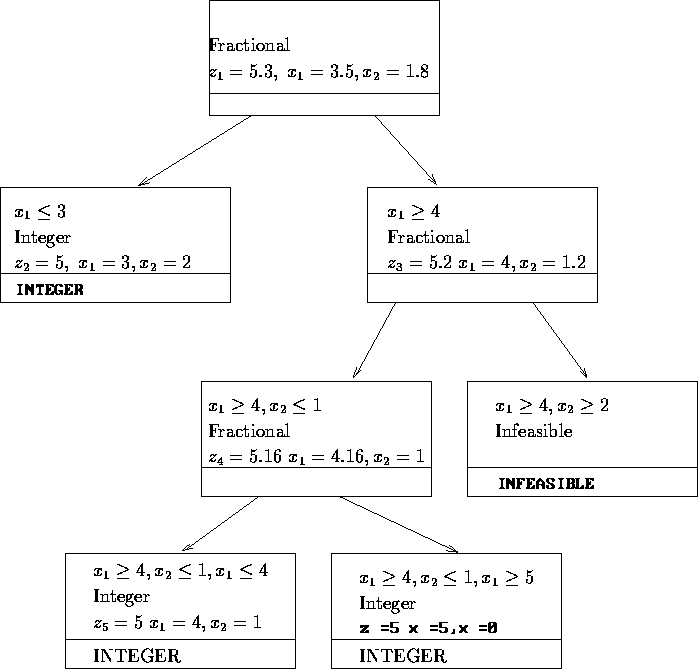
each with value z=5.
Exercise 6
From the enumeration tree of Exercise 5, we see that only one branching is
necessary since both subproblems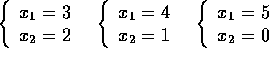 
and 
are inactive by reason of
integrality. The better solution is 
with value 
.
Exercise 7
MAX 4 X1 + 7 X2 + 6 X3 + 5 X4 + 4 X5
SUBJECT TO
2) 5 X1 + 8 X2 + 3 X3 + 2 X4 + 7 X5 <= 112
3) X1 + 8 X2 + 6 X3 + 5 X4 + 4 X5 <= 109
END
GIN 5
ENUMERATION COMPLETE. BRANCHES= 6 PIVOTS= 20
OBJECTIVE FUNCTION VALUE 151.000
VARIABLE VALUE REDUCED COST
X1 14.000 -4.000
X2 .000 -7.000
X3 .000 -6.000
X4 19.000 -5.000
X5 .000 -4.000
Exercise 8
Since 
does not satisfy the knapsack constraint
, it follows that 
must hold for all solutions of the knapsack problem.
Similarly for 
.
MAX 8 X1 + 11 X2 + 6 X3 + 4 X4
SUBJECT TO
2) 5 X1 + 7 X2 + 4 X3 + 3 X4 <= 14
3) X1 + X2 + X3 <= 2
3) X1 + X2 + X4 <= 2
END
SUB X1 1
SUB X2 1
SUB X3 1
SUB X4 1
OBJECTIVE FUNCTION VALUE 21.000
VARIABLE VALUE REDUCED COST
X1 .000 0.000
X2 1.000 -3.000
X3 1.000 -2.000
X4 1.000 0.000
Exercise 9.
(a) Nearest Neighbor starting from city 1 yields the tour
1 - 4 - 8 - 9 - 10 - 13 - 14 - 11 - 12 - 15 - 7 - 5 - 6 - 2 - 3 - 1
of length 89.
Applying 2-opt, we get the following improvements: replace 1-3 and 2-6 by 1-2 and 3-6 for a gain of 6. The new tour is
1 - 2 - 3 - 6 - 5 - 7 - 15 - 12 - 11 - 14 - 13 - 10 - 9 - 8 - 4 - 1
Replace 3-6 and 5-7 by 3-5 and 6-7 for a gain of 2. The new tour
1 - 2 - 3 - 5 - 6 - 7 - 15 - 12 - 11 - 14 - 13 - 10 - 9 - 8 - 4 - 1
has lenth 81.
(b) We start Nearest Insertion with the tour 5 - 6 - 5 of length 6.
Then we insert city 7 at a cost of 4+5-3=6 (note that there is a tie. We could have inserted city 9 instead). The new tour is 5 - 6 - 7 - 5. Then the nodes are inserted in the following order: 9 (between 6 and 7), 11 (between 7 and 9), 12 (between 7 and 11), 10 (between 9 and 11), 14 (between 10 and 11), 8 (between 9 and 10), 13 (between 8 and 10), 4 (between 8 and 9), 2 (between 4 and 9 ), 1 (between 2 and 4), 15 (between 11 and 12) and finally 3 (between 5 and 7). The resulting tour is
1 - 2 - 9 - 6 - 5 - 3 - 7 - 12 - 15 - 11 - 14 - 10 - 13 - 8 - 4 - 1
and has length 79. There is no improvement with 2-opt.
(c) We start Furthest Insertion with the tour 1 - 15 - 1 of length 46. Then city 3 is inserted followed by city 13. The new tour is 1 - 3 - 15 - 13 with length 60. The remaining nodes are inserted in the folowing order: 6 (between 13 and 15), 14 (between 6 and 13), 5 (between 6 and 15), 11 (between 5 and 15), 7 (between 5 and 11), 10 (between 13 and 14), 9 (between 6 and 14), 12 (between 11 and 15), 12 (between 11 and 15), 4 (between 1 and 13), 8 (between 4 and 13) and finally 2 (between 1 and 3). The resulting tour
1 - 2 - 3 - 15 - 12 - 11 - 7 - 5 - 6 - 9 - 14 - 10 - 13 - 8 - 4 - 1
has length 81. There is no improvement with 2-opt.
(d) We take as the central point on the map the midpoint between 5 and 10. The resulting tour obtained by applying the sweep heuristic is
7 - 3 - 5 - 6 - 2 - 1 - 4 - 8 - 9 - 13 - 10 - 14 - 11 - 15 - 12 - 7
and it has length 80.
Applying the 2-opt heuristic, we replace 9-13 and 10-14 by 9-10 and 13-14, thus reducing the length of the tour by 1. The new tour
1 - 2 - 6 - 5 - 3 - 7 - 12 - 15 - 11 - 14 - 13 - 10 - 9 - 8 - 4 - 1
has length 79.