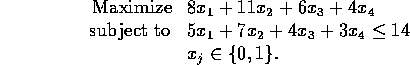
The knapsack problem is a particularly simple integer program: it has only one constraint. Furthermore, the coefficients of this constraint and the objective are all non-negative. For example, the following is a knapsack problem:
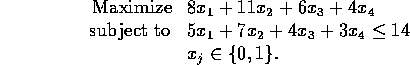
The traditional story is that there is a knapsack (here of capacity 14). There are a number of items (here there are four items), each with a size and a value (here item 2 has size 7 and value 11). The objective is to maximize the total value of the items in the knapsack. Knapsack problems are nice because they are (usually) easy to solve, as we will see in the dynamic programming section of this course.
To solve the associated linear program, it is simply a matter of
determining which variable gives the most ``bang for the buck''. If
you take 
(the objective coefficient/constraint coefficient)
for each variable, the one with the highest ratio is the best item to
place in the knapsack. Then the item with the second highest ratio is
put in and so on until we reach an item that cannot fit. At this
point, a fractional amount of that item is placed in the knapsack to
completely fill it. In our example, the variables are already ordered
by the ratio. We would first place item 1 in, then item 2, but item 3
doesn't fit: there are only 2 units left, but item 3 has size 4.
Therefore, we take half of item 3. The solution 
, 
,
, 
is the optimal solution to the linear program.
As already observed in Section 2.1, this solution is quite different from the optimal solution to the knapsack problem. Nevertheless, it will play an important role in the solution of the problem by branch and bound as we will see shortly.