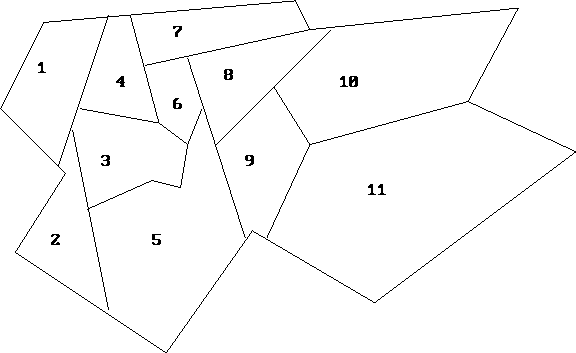
Figure 1: Map of the city
To illustrate this model, consider the following location problem: A city is reviewing the location of its fire stations. The city is made up of a number of neighborhoods, as illustrated in Figure 1.
A fire station can be placed in any neighborhood. It is able to handle the fires for both its neighborhood and any adjacent neighborhood (any neighborhood with a non-zero border with its home neighborhood). The objective is to minimize the number of fire stations used.
We can create one variable ![]() for each neighborhood j. This
variable will be 1 if we place a station in the neighborhood, and
will be 0 otherwise. This leads to the following formulation
for each neighborhood j. This
variable will be 1 if we place a station in the neighborhood, and
will be 0 otherwise. This leads to the following formulation
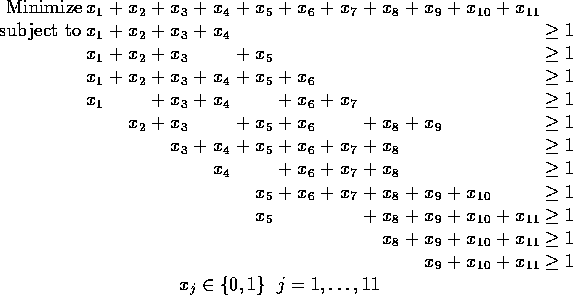
The first constraint states that there must be a station either in
neighborhood 1 or in some adjacent neighborhood. The next constraint
is for neighborhood 2 and so on. Notice that the constraint
coefficient ![]() is 1 if neighborhood i is adjacent to
neighborhood j or if i=j and 0 otherwise. The jth column of the
constraint matrix represents the set of neighborhoods that can be
served by a fire station in neighborhood j. We are asked to find a
set of such subsets j that covers the set of all
neighborhoods in the sense that every neighborhood appears in the
service subset associated with at least one fire station.
is 1 if neighborhood i is adjacent to
neighborhood j or if i=j and 0 otherwise. The jth column of the
constraint matrix represents the set of neighborhoods that can be
served by a fire station in neighborhood j. We are asked to find a
set of such subsets j that covers the set of all
neighborhoods in the sense that every neighborhood appears in the
service subset associated with at least one fire station.
One optimal solution to this is ![]() and the
rest equal to 0.
and the
rest equal to 0.
This is an example of the set covering problem. The set
covering problem is characterized by having binary variables, ![]() constraints each with a right hand side of 1, and having simply sums
of variables as constraints. In general, the objective function can
have any coefficients, though here it is of a particularly simple form.
constraints each with a right hand side of 1, and having simply sums
of variables as constraints. In general, the objective function can
have any coefficients, though here it is of a particularly simple form.