Our final relaxation is based on a completely different idea. We can arbitrarily orient a tour and talk in terms of node j following node i. Clearly each node follows exactly one other node and is followed by one other node. This leads to an assignment problem.
We know that 
is the cost of having node j follow node i.
If we form the assignment problem in figure 4, then we can
find the best way to determine which node should follow which. The
solution is also given in figure 4.
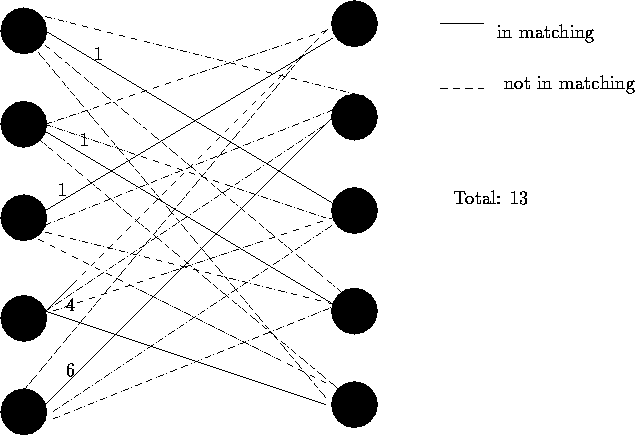
Figure 4: Assignment Formulation and Solution
At first glance, it might seem that this solves the TSP. Actually, there is a problem because the ``solution'' is actually two subtours of the nodes: one from B to D to E to B, and one from A to C to A. This relaxation has removed the restriction that the tour must be in one piece. But, because it includes all possible tours, including the optimal one, the assignment cost is a valid lower bound on the cost of an optimal tour. This implies that no tour has length less than 13 (which we already knew from the one-tree relaxation).