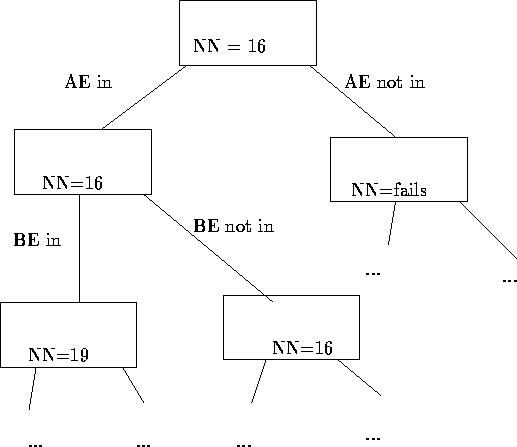
Figure 5: Branching without bounding
It is clear that examining relaxations and heuristics together is a valuable thing to do. In our example, we are able to state that nearest neighbor is within two of optimum, even though we are not certain what the optimum is (it turns out to be 15). We can combine heuristics and relaxations in a more powerful way that gives a reasonable chance for finding the optimal solution within a relatively short amount of time (relative to the age of the universe, anyway). This method is called branch and bound. You know branch and bound in the context of integer programming. This generalizes the ideas.
Suppose we wanted to enumerate all the tours in our problem. One method would be to continually divide the solution space into smaller and smaller sets until our heuristic restricted to the set returns the optimal tour in that set. There are many ways we can divide the solution set. One choice is to choose an arc (i,j) and form two sets: one for solutions where (i,j) is in the tour, and one for which (i,j) is not in the tour. This is an example of branching. Figure 5 illustrates the branching process, where I have arbitrarily selected edges to divide the solutions and I have applied the nearest neighbor heuristic to each of the restricted sets.

Figure 5: Branching without bounding
This branching provides an organized way to search through the solution space. As long as our heuristic can find the optimal answer to a solution set with only one tour in it (and nearest neighbor can), the optimal tour will eventually be found.
Fortunately, we can do more by also running our relaxation for each of the solution sets. Suppose we have found a feasible tour with value c'. Then, if we are able to show that the best tour in some solution set is no better than c', we need no longer divide that solution set. Such a solution set is said to be fathomed. In many practical situations, if both the heuristic and relaxation tend to give solutions that are close to the optimal value, many, many sets will become fathomed, and the amount of work that has to be done will be very small. Figure 6 shows how fathoming is done in our example. If both AE and BE are in the solution, the best that can be hoped for is a solution with value 16. Since we already have a solution with value 16, we can fathom this solution set.
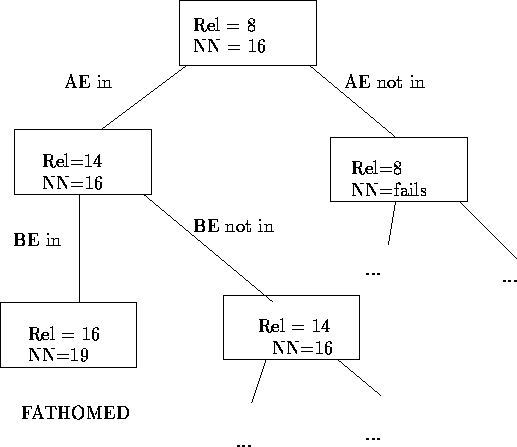
Figure 6: Branching with bounding
In general, branch and bound works as follows:
1) Solve the problem with a heuristic and a relaxation. Let the heuristic value be c'. If the relaxation value is also c', then stop, your heuristic solution is optimal. Form a branch and bound tree with a single node in it representing the entire solution set. Mark this node discovered and unexamined.
2) Choose an unexamined node in the branch and bound tree. If no examined node exists go to 5. If the node is discovered, go to 4, else go to 3.
3) (Node is undiscovered) Run the heuristic and the relaxation on the solution set represented by the node. If the heuristic value is less than c' then let c' equal the heuristic value. Mark the node discovered. Go to step 2.
4) (Node is discovered) Mark this node examined. If the relaxation value at this node is at least c' go to step 2. Otherwise, divide the solution set at the node into two nodes, add them to the branch and bound tree, mark both undiscovered and unexamined. Go to step 2.
5) (Stop) Stop, c' gives the optimal solution value.
This is a very rough outline of branch and bound. There is a lot of work on which branching rules work and which do not and on which unexamined node to choose in step 2. No matter how you make these decisions, though, it is possible that you will look at a tremendous number of possible solutions before finding the optimal solution.