Further to yesterday’s entry, we can now determine exactly how much of the podium Canada owns. To determine the “winner” of the Olympics, you need to determine the relative values of gold, silver, and bronze medals (with the assumption that non-medalers do not count, which is arguably false, but necessary in order to stop me from spending the night compiling broader lists). The final medal standings are (from nbcolympics.com):
| Country | Medalists | Total | ||||
|---|---|---|---|---|---|---|
| United States | See Names | 9 | 15 | 13 | 37 | |
| Germany | See Names | 10 | 13 | 7 | 30 | |
| Canada | See Names | 14 | 7 | 5 | 26 | |
| Norway | See Names | 9 | 8 | 6 | 23 | |
| Austria | See Names | 4 | 6 | 6 | 16 | |
So, if you count every medal equally, then the USA won; if you only count gold, Canada won. But what if you count things 5 for a gold, 3 for a silver, and 1 for a bronze? Then the USA wins. How about 10, 5, 1? That would be Canada. Is there a set of points for Germany to win? It turns out there is not: anyone with operations research training would fiddle around for a while and figure out that 3/4 of the US medals plus 1/4 of the Canadian medals dominates the German medal counts. Everyone else is dominated by the USA: only Canada and the USA might win for a given set of medal weights.
Now not every point system makes sense. Giving 10 points for a bronze and 1 point for a gold might match up with certain egalitarian views, but would not really be in keeping with a competition. So we can limit ourselves to point systems with gold >= silver >= bronze. Further, we can normalize things by making the weights add up to 1 (since multiplying a weighting by a constant number across the scores doesn’t change the ordering) and having the weights be non-negative (since getting a medal shouldn’t hurt your score).
This gives a base set of linear equalities/inequalities. If we let wg, ws, and wb be the weights for gold, silver and bronze, we are interested in weights which satisfy
wg >= ws >= wb
wg+ws+wb = 1
wg, ws, wb >= 0
Now, which weights favor Canada? It turns out that, with some basic algebra, you can deduce (using the medal counts above) that Canada wins whenever wg > 8/13 (and ties with wg=8/13). So as long as you put more than 61.5385% of the weight on gold, Canada wins. This amounts to about 45.25% of the feasible region. USA wins on the remaniing 54.75% of the region. If Canada had won one more silver medal, they would have prevailed on more than half the reasonable region.
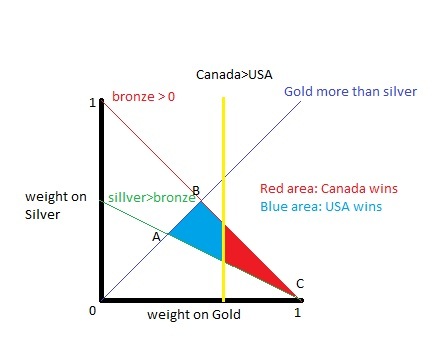 The diagram illustrates the weights for the USA and Canada, giving only the weights for gold and silver (the weight for bronze is 1-gold-silver). The red region are the weights where Canada wins; the blue is for the USA. Point A is “all medals are equal”; Point B is “count only gold and silver”; Point C is “Count only gold”. The yellow line corresponds to the weight on gold equaling 8/13.
The diagram illustrates the weights for the USA and Canada, giving only the weights for gold and silver (the weight for bronze is 1-gold-silver). The red region are the weights where Canada wins; the blue is for the USA. Point A is “all medals are equal”; Point B is “count only gold and silver”; Point C is “Count only gold”. The yellow line corresponds to the weight on gold equaling 8/13.
Bottom line: on this measure, the USA won the Olympics in an extraordinarily close race. Canada may not have “Owned the Podium” but they came darn close.
What if you use the metric medal/population?
I think for all sports, there’s a perfectly well-defined 4th place. It’s sort of arbitrary that the “chocolate medal” always counts 0 whereas the gold/silver/bronze are strictly positive… what if you re-weight your statistics in that way? What about the top 5???
Mike,
Excellent analysis. As you know the Government of Canada plowed $ 100 m + into the “Own the Podium” program (a lot for Canada). They set the goal of getting the highest medal count. If you look strictly at that one dimensional goal the program looks like an abject failure. However if you look at your analysis you could make an argument that the program achieved over 90% of it’s goal.
Goal setting is a tricky. Presenting the results almost as tricky.
Luigi,
by that metric, among the top 5, Norway crushes everybody else. Here it is in medals per million: http://spreadsheets.google.com/ccc?key=0AthXQWuTea4MdDk1OTZsNk1WaHpXenVaRENJWkVMX3c&hl=en (fee free to add countries to the list if you want, anybody can edit)
I should note that I don’t think that’s a reasonable measure at all, but it is fun.
Interesting take that provides good background to understand the somewhat arbitrary issue of medal rankings. There are several approaches that are used by various instances:
1. Gold medal total (tends to be of little use below the top 4-5 nations – too many ties, too few gold medals)
2. Medal total (does not differentiate between medals)
3. Medal point total (5 for gold, 3 for silver, 1 for bronze)
4. Total top8 finishes: (useful to look at conversion rate: what % of a nation’s total top8s are medals)
5. Top8 points total (also known as Honour points – 10, 8, 6, 5, 4, 3, 2,1) awarded to the top 8 finishes in each medal event.
The first 3 approaches focus on medals and therefore a generally accepted measure of Olympic success. The last 2 approaches focus on depth: how deep is Nation X in winter sports or in sport Y.
The Medal Point ranking has the advantage, as pointed out in the article, to address both the quantity (how many medals won) and the quality (how valuable: i.e. where Gold > Silver > Bronze). In the case of the Vancouver Games, USA comes out on top with 103 points (9 gold x 5pts)+(15 silver x 3pts) + 13 bronze = 103. Under this system, Germany and Canada come out tied with 96 points. The number of gold is usually used to break ties, if the tie remains, then the number of silver, etc.
Great analysis,
We’ve heard much talk about this being the most medals the US has ever won in the Winter Olympics, but the next sentence is usually the caveat that there are more games than ever before.
If you can find the time, it would be great to see a historical comparison of percentage of the podium with the variable weighting as you’ve done here. If I have the time, I’ll probably just do a simple, each medal is equal weighting.
Nate Silver of fivethirtyeight.com–mostly an excellent source of analysis of political data–did an analysis of medal counts that addresses the question Patrick raised.
Mike might also know of Nate, who started as a baseball statistics analyst before he dove into analyzing political polls in the 2008 presidential election.
One thing that isn’t clear to me is why we should prefer the area determined by one set of variables to another. I took a look at a few other options to see if we could help Canada declare itself the winner.
1. Use the same system as Mike, but look at the projection onto (silver, bronze) or (gold, bronze). These are just affine transformations of the existing variables, so they preserve relative areas, I think. No change.
2. Use the variables s = ratio of silver/gold, b = ratio of bronze/silver. Then the unit square is the set of all possibilities, and Canada wins for s <= 5/8 * 1/(1+b). If I did it right, that works out to 43.3%. Not too different.
3. Use the variables s = ration of silver/gold, b = ratio of bronze/gold. The base set is half the unit square, because of b <= s. Canada wins for s + b <= 5/8. Unfortunately that's only 19.5% of the area! Better not use that one–it's a little less intuitive in my mind anyway.
Oh well.
5,3,1 is a bit unfair on bronze. I prefer 4,2,1 where the next medal is twice as good as the previous.
This helps Canada by by just a very tiny amount but the US still wins.
Countries don’t win Olympics. Athletes win Olympic medals. Period.
Your detailed analysis shows how much you don’t get it.
Hey Jon, Thanks for the feedback. Glad you stopped by: a ray of light in the blogoverse.
Wow!–really cool analysis here Michael. I wonder what the results would look like if we used the market values for how weighing the different medals.
I know the formatting will stink, (but it should be copy-and-paste-able) and I didn’t weight the medals, but this table shows percentage of medals won by the US out of medals available to win, in Winter Olympics, going back to 1988. I assume 3 medals per event. Event counts via wikipedia. Medal counts from databaseolympics.com (no affiliation, I just did a web search for olympic results and they came up).
Location Year Sports Events Medals US Percent
Calgary 1988 6 46 138 6 4%
France 1992 7 57 171 11 6%
Norway 1994 6 61 183 13 7%
Japan 1998 7 68 204 13 6%
Salt Lake 2002 7 78 234 34 15%
Italy 2006 7 84 252 25 10%
Vancouver 2010 7 86 258 37 14%
btw, with this crude measure, Canada’s 26 in 2010 is 10%. I didn’t do it to measure country vs. country, but rather to see if the 37 medals won by the US is truly over-inflated due to there being more events in 2010 than ever before, or if it actually shows improved performance. Matthew, thanks for that link to 538. Nate did a good job of handling the new events vs. classic events question.
It’s interesting that the 37 won in 2010 is more than the 34 won in Salt Lake City, but it’s not as much of a percentage of the available medals as the US won in Salt Lake City.
On the other hand,. it is the most by any country in these 2010 games, whereas the Salt Lake total was second best. The Germans had the most in Salt Lake 2002.
So if the question is, did the US have a better performance in 2002 or 2010, the answer is fairly debatable.
Does anyone besides me think we should set this up as a DEA model and let each country select weights that most favors them (subject to nonnegativity and ordering restrictions)? We should also let them define inputs. Population and budget have already been mentioned, but what about local snowfall? (I’m thinking of the skier from Ghana that was written up in Sports Illustrated. Not to mention the famed Jamaican bobsled team.)
Very informative one , Is there any official point system exists for medals
There is no official point system. As Jon rather snottily pointed out in comment 10, it is the athletes who win medals. The country ranking is really just for fun.
I am confused by the wg = 8/13 condition for equality – shouldn’t this also depend on ws, i.e. give a line of finite slope? Excuse my naivety.
J.
John: normally it would also involve ws. As the numbers happened to work out, the weight for ws came out as 0 (this is because the teams differ by 2 for both silver and bronze: if they differ by the same amount, then it doesn’t matter whether you assign weight to silver or bronze). Just a coincidence this time that things canceled out.
Ah sure, thanks. I should have noticed that, or worked it through properly myself 🙂