Like many in operations research, my research interests often creep over into my everyday life. Since I work on scheduling issues, I get particularly concerned with everyday scheduling, to the consternation of my friends and family (“We should have left six minutes ago: transportation is now on the critical path!”). This was particularly true when I was a doctoral student when, by academic design, I was living and breathing operations research 24 hours a day.
I was a doctoral student from ages 22 to 27 (age will be relevant shortly), and like many in that age group, I was quite concerned with finding a partner with whom to spend the rest of my life. Having decided on certain parameters for such a partner (female, breathing, etc.), I began to think about how I should optimally find a wife. In one of my classes, it hit me that the problem has been studied: it is the Secretary Problem! I had a position to fill (secretary, wife, what’s the difference?), a series of applicants, and my goal was to pick the best applicant for the position.
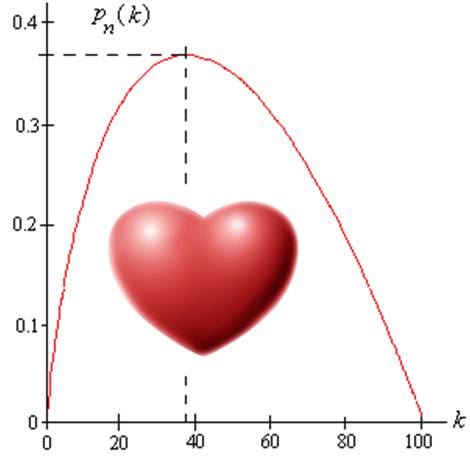 Fortunately, there is quite a literature on the Secretary Problem (for a very nice summary of results, see this site, from which I also got the background to the graphic for this entry), and there are a number of surprising results. The most surprising is that it is possible to find the best secretary with any reasonable probability at all. The hard part is that each candidate is considered one at a time, and an immediate decision must be made to accept or reject the candidate. You can’t go back and say “You know, I think you are the cat’s meow after all”. This matched up with my empirical experience in dating. Further, at each step, you only know if the current candidate is the best of the ones you have seen: candidates do not come either with objective values or with certifications of perfection, again matching empirical observations. You can only compare them with what you have sampled.
Fortunately, there is quite a literature on the Secretary Problem (for a very nice summary of results, see this site, from which I also got the background to the graphic for this entry), and there are a number of surprising results. The most surprising is that it is possible to find the best secretary with any reasonable probability at all. The hard part is that each candidate is considered one at a time, and an immediate decision must be made to accept or reject the candidate. You can’t go back and say “You know, I think you are the cat’s meow after all”. This matched up with my empirical experience in dating. Further, at each step, you only know if the current candidate is the best of the ones you have seen: candidates do not come either with objective values or with certifications of perfection, again matching empirical observations. You can only compare them with what you have sampled.
Despite these handicaps, if you know how many candidates there are, there is a simple rule to maximize the chance of finding the best mate: sample the first K candidates without selecting any of them, and then take the first subsequent candidate who is the best of all you have seen. K depends on N, the total number of candidates you will see. As N gets big, K moves toward 1/e times N, where e is 2.71…. So sample 36.9% of the candidates, then take the first candidate who is the best you have seen. This gives a 36.9% chance of ending up with Ms (in my case) Right.
One problem here: I didn’t know what N is. How many eligible women will I meet? Fortunately, the next class covered that topic. If you don’t know what N is but know that you will be doing this over a finite amount of time T, then it is OK to replace this with a time cutoff rule: simply take the first candidate after 36.9% of the time (technically, you use 36.9% of the cumulative distribution, but I assumed a uniform distribution of candidate arrivals). OK, I figured, people are generally useless at 40 (so I thought then: the 50-year-old-me would like to argue with that assumption), and start this matching process at about 18 (some seem to start earlier, but they may be playing a different game), so, taking 36.9% of the 22 year gap gives an age of 26.11. That was my age! By a great coincidence, operations research had taught me what to do at exactly the time I needed to do that.
Redoubling my efforts, I proceeded to sample the candidate pool (recognizing the odds were against me: there is still only a 36.9% chance of finding Ms Right) when lo and behold. I met Her: the woman who was better than every previous candidate. I didn’t know if she was Perfect (the assumptions of the model don’t allow me to determine that), but there was no doubt that she met the qualifications for this step of the algorithm. So I proposed.
And she turned me down.
And that is when I realized why it is called the Secretary Problem, and not the Fiancee Problem (though Merrill Flood proposed the problem under that name). Secretaries have applied for a job and, presumably, will take the job if offered. Potential mates, on the other hand, are also trying to determine their best match through their own Secretary Problem. In order for Ms Right to choose me, I had to be Mr. Right to her! And then things get much more complicated. What if I was meeting women in their sampling phase? It did seem that some people were very enthusiastic about having long sampling phases, and none of them would be accepting me, no matter how good a match they would be for me. And even the cutoff of 36.9% looks wrong in this case. In order to have a hope of matching up at all in this “Dual Secretary Problem”, it looked like I should have had a much earlier cutoff, and in fact, it seemed unlikely there was a good rule at all!
I was chagrined that operations research did not help me solve my matching problem. I had made one of the big mistakes of practical operations research: I did not carefully examine the assumptions of my model to determine applicability.
Downcast, I graduated with my doctorate, resolving to marry myself to integer programming. I embarked on a postdoc to Germany.
There, I walked into a bar, fell in love with a beautiful woman, moved in together three weeks later, invited her to live in the United States “for a while”, married her six years after that, and had a beautiful son with her six years ago. I am not sure what optimization model led me down that path, but I think I am very happy with the result.
Some details of this story have been changed to protect me from even more embarrassment. This post is part of the February INFORMS Blog Challenge.
“Life is what happens to you while you’re busy making other plans.” — John Lennon
My first paper was on the secretary problem…
http://www.princeton.edu/~rvdb/tex/myPapers/OptimalChoice.pdf
My thesis advisor (Dynkin) asked if I could solve the variant of the problem in which one gets to pick the best k out of n (think polygamy). Among other things, it turns out that one can pick the best k out of n=2k with probability 1/(k+1). I also showed that you can pick the 2nd best (the best will marry the high-school jock) with probability 1/4 exactly!
Mike – I like it.
I’ve had to lift one line of argument from this to use in our follow up post to ‘Cupids with Computers’…
http://blogs.uk.capgemini.com/orblog/2011/02/25/cupids-with-computers/
http://blogs.uk.capgemini.com/orblog/2011/03/02/two-deadly-sins/
Michael, I have just found your blog. My 2c: It seems like a Ph.D. thesis in the OR of Romance would be a shoe-in for the eHarmony research department 🙂
I told my wife I met her when I was 26. She went like , “so what? one of my colleagues just got devoiced, and they got married at the age 26”.
Only seeing this post now (have been very busy lately) and just LOVE it! Which, I guess, is the perfect reaction for a post on OR and love! Great story on how you met your wife.