I have come across a couple of items recently involving market rationality and the ability of the market to reflect “unknown” information. The first came in a conversation with my colleague Bryan Routledge. Harkening back to the Challenger disaster, Bryan mentioned that “the market” quickly determined the company that caused the failure (all this is my paraphrasing of my understanding of what Bryan said: it is my fault if it is wrong!). Here is the graph of the stock prices of the main companies involved in building the space shuttle on the day of the disaster:
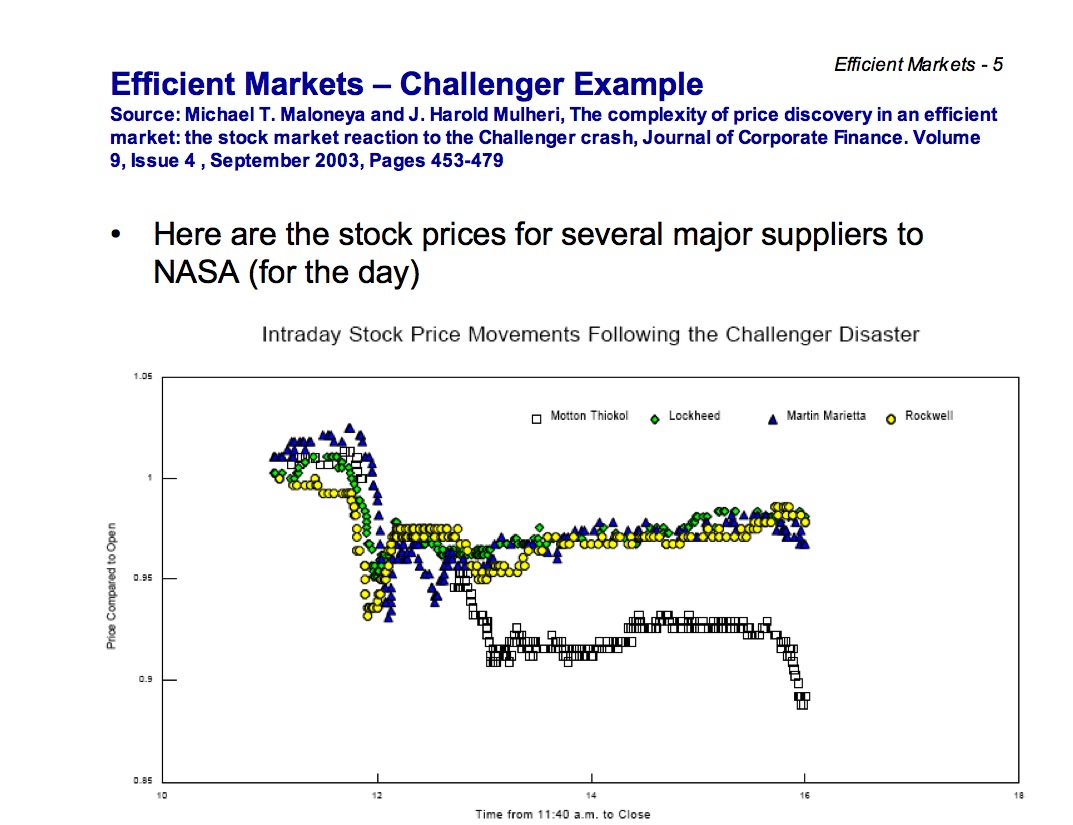
There are four companies shown: Morton Thiokol, Lockheed, Martin Marietta, and Rockwell. The stock price for all of the companies immediately dropped 7-8% after the disaster. Within an hour, three companies went back up to being just 2-3% down, while one company further decreased: Morton Thiokol. The company responsible for the O-ring (of Richard Feynman and ice water fame): Morton Thiokol. It is certainly provocative that the market seemed to know something immediately that took an investigation months to determine. It would have been even more impressive if the market identified this an hour earlier (the explosion happened at 11:39AM), but the results from the day are still pretty impressive.
But, as Bryan reminds me, this was not exactly a mystery to everyone at the time: the engineers involved strongly suspected early what the issue was and later fed that information to Feynman. So the information was out there and perhaps that information leaked out to the market in the immediate aftermath of the explosion. So perhaps it is not so mysterious after all. And there may well be other explanations for the larger drop off by Motton Thiokol.
Continuing the theme of markets seeming to have information that mere mortals do not, Panos Ipierotis, with tongue-in-cheek, suggested a prediction market on the P=NP question, arguing
So,if P=NP is a decidable problem, it is either true or false. So, a fully rational agent, participating in the market, should know whether P=NP. It is not a matter of probabilities! All the information to make the decision is available. So, if the market has one or more rational players, the market should converge to a price of 0 or 1 immediately, depending on the state of the problem. Right?
He then offers a few choices when the market, presumably, does not give such a result:
- There are no rational agents. So, all the analysis of prediction markets that assume rationality of traders is incomplete.
- There are rational agents. The market does not converge to 0 or 1 because the P=?NP problem is undecidable.
- There are rational agents but the return from the risk-free rate until reaching the time to settlement exceeds the return from the market. So, the market gives information on how long it will take for the problem to be officially solved.
- If your laptop cannot find the solution, neither can the market.
These are not mutually exclusive: it could be more than one. But I think it is pretty clear that there are no rational agents by this definition, and I think most or all economists will agree to that. The concept of having a rational agent is no different than the assumption of linearity and divisibility and so on in linear programming. A model cannot include everything (a map that includes everything would be as large as the area mapped), so simplifications are made. Some economic models include limits on rationality, or on information, or on timing, while others will give their agents more power/information/etc. than could occur in practice. There is normally a tradeoff: with more detail on rationality may come limits in other areas, such as number of agents, or complexity of markets. Given some set of assumptions, it is pretty easy to come up with a situation that exploits weaknesses in the assumptions. If that is the case, those are the wrong assumptions to make!
So I would agree with Panos: “all the analysis of prediction markets that assume rationality of traders is incomplete”. That “incomplete” analysis might still be useful. To paraphrase the statistician George Box: all models are incomplete; some are useful.
This concept was certainly seen by Feynman in the Challenger case when he questioned whether some of the mathematical models used were useful. From Feynman’s appendix to the Challenger Report:
When using a mathematical model careful attention must be given to uncertainties in the model.
I really enjoyed this post – in particular the paraphrase of George Box. I’ve gotta remember that one…
Mike, nice analysis! I could not agree more. One note about the Feynman quote that you end with–I wish he had said “careful attention must be given to uncertainties ABOUT the model.” The difference is subtle but important, particularly if one is modeling uncertainty explicitly. But I suspect that Feynman understood this better than most people!
Don
You’re right about economists and rationality. In fact, thanks to the Nobel Prizes in Economics related to Psychology loads of us are starting to think ‘there’s no such thing as a rational agent’.
As per the application to the stock markets, classified information and missed variables (this is BS, simply means the former) are good pieces that allow the stock price to aggregate the information.