Operations Research, Sudoko, Rogo, and Puzzles

A few years back, Sudoko became a craze with seemingly everyone spending their time solving these puzzles.  The puzzle is quite simple:  take a nine by nine grid, partially filled in with numbers from one to nine, and complete it so that every row, column, and non-overlapping 3×3 square contains the numbers one through nine exactly once each.  While the grid contains numbers, there is no mathematics involved:  using the letters a-i would work as well.  But you can use mathematics (in the form of logic) to solve the puzzle.  To solve these by hand, puzzlers quickly learn logical rules, from the simple (“If only one square is open in a row, then you know what number goes there”) to advanced (say, alternate pair exclusion).  One can even use the methods of operations research (say, constraint programming or integer programming) to solve Sudoko puzzles.   It does not seem to discourage human solvers to know that these techniques can solve any Sudoko problem in milliseconds.

There is often a close relationship between puzzles and the methods of operations research, particularly networks or discrete mathematics.  Finding a path in a maze is nothing more than a shortest path problem;  “logic” puzzles (“Smith, Jones, and Robinson are (not respectively) a trucker, a fireman, and an engineer, who live in …”, followed by facts, leading to “What is the name of the engineer?”) can be handled through integer programming, and so on.  People, for some reason, like to do combinatorial search in their spare time.

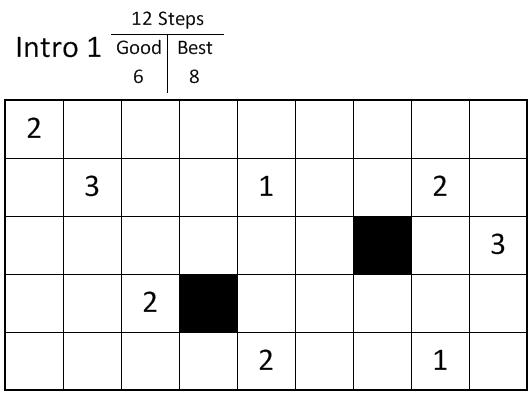
Hamish Waterer, with whom I shared an office in New Zealand and who is now at Newcastle in Australia, pointed out to me a puzzle that has even closer ties to operations research: Rogo.  In Rogo, the goal is to find a loop through a grid of fixed length that contains as many reward points as possible.    So, for this example (taken from the Rogo site)

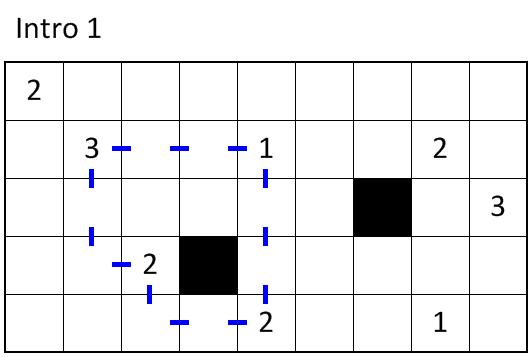
the goal in this example is to find a loop of no more than 12 steps that includes as many points as possible.   The loop must be a real loop:  it must return where it started and can’t cross itself or double back. Steps can be either horizontal or vertical:  they cannot be diagonal.  The loop cannot include any of the black squares.  Here is the solution:

Rogo was created by two faculty members (Nicola Petty and Shane Dye)  at the University of Canterbury in Christchurch, New Zealand.  Not surprisingly, Nicola and Shane teach management science there:  the problem has a very strong operations research flavor.  This is a form of the Prize Collecting Traveling Salesman problem, originally studied by my colleague Egon Balas (in the regular PCTSP, there is a penalty for distance traveled:  in Rogo, there is an upper bound).

If you want to play around with this, you can get the iPhone (touch, pad, etc.) app. Creating a solver would make a nice undergraduate project (and I suspect there are at least a few master’s theses and perhaps a doctoral dissertation on algorithmic aspects of creating and solving these).